5 5 | CONTINUOUS RANDOM VARIABLES

Figure 5.1 The heights of these radish plants are continuous random variables. (Credit: Rev Stan)

Introduction

NOTEThe values of discrete and continuous random variables can be ambiguous. For example, if X is equal to the number of miles (to the nearest mile) you drive to work, then X is a discrete random variable. You count the miles. If X is the distance you drive to work, then you measure values of X and X is a continuous random variable. For a second example, if X is equal to the number of books in a backpack, then X is a discrete random variable. If X is the weight of a book, then X is a continuous random variable because weights are measured. How the random variable is defined is very important.
Continuous random variables have many applications. Baseball batting averages, IQ scores, the length of time a long distance telephone call lasts, the amount of money a person carries, the length of time a computer chip lasts, rates of return from an investment, and SAT scores are just a few. The field of reliability depends on a variety of continuous random variables, as do all areas of risk analysis.

| Properties of Continuous Probability Density Functions

The graph of a continuous probability distribution is a curve. Probability is represented by area under the curve. We have already met this concept when we developed relative frequencies with histograms in Chapter 2. The relative area for a range of values was the probability of drawing at random an observation in that group. Again with the Poisson distribution in Chapter 4, the graph in Example 4.14 used boxes to represent the probability of specific values of the random variable. In this case, we were being a bit casual because the random variables of a Poisson distribution are discrete, whole numbers, and a box has width. Notice that the horizontal axis, the random variable x, purposefully did not mark the points along the axis. The probability of a specific value of a continuous random variable will be zero because the area under a point is zero. Probability is area.

The curve is called the probability density function (abbreviated as pdf). We use the symbol f(x) to represent the curve. f(x) is the function that corresponds to the graph; we use the density function f(x) to draw the graph of the probability distribution.

Area under the curve is given by a different function called the cumulative distribution function (abbreviated as cdf). The cumulative distribution function is used to evaluate probability as area. Mathematically, the cumulative probability density function is the integral of the pdf, and the probability between two values of a continuous random variable will be the integral of the pdf between these two values: the area under the curve between these values. Remember that the area under the pdf for all possible values of the random variable is one, certainty. Probability thus can be seen as the relative percent of certainty between the two values of interest.

• The outcomes are measured, not counted.
• The entire area under the curve and above the x-axis is equal to one.
• Probability is found for intervals of x values rather than for individual x values.
• P(c < x < d) is the probability that the random variable X is in the interval between the values c and d. P(c < x < d) is the area under the curve, above the x-axis, to the right of c and the left of d.
• P(x = c) = 0 The probability that x takes on any single individual value is zero. The area below the curve, above the x-axis, and between x = c and x = c has no width, and therefore no area (area = 0). Since the probability is equal to the area, the probability is also zero.
• P(c < x < d) is the same as P(c ≤ x ≤ d) because probability is equal to area.

We will find the area that represents probability by using geometry, formulas, technology, or probability tables. In general, integral calculus is needed to find the area under the curve for many probability density functions. When we use formulas to find the area in this textbook, the formulas were found by using the techniques of integral calculus.

There are many continuous probability distributions. When using a continuous probability distribution to model probability, the distribution used is selected to model and fit the particular situation in the best way.

In this chapter and the next, we will study the uniform distribution, the exponential distribution, and the normal distribution. The following graphs illustrate these distributions.

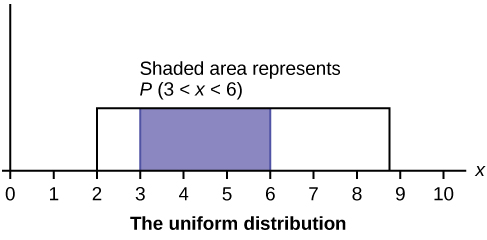
Figure 5.2 The graph shows a Uniform Distribution with the area between x = 3 and x = 6 shaded to represent the probability that the value of the random variable X is in the interval between three and six.

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

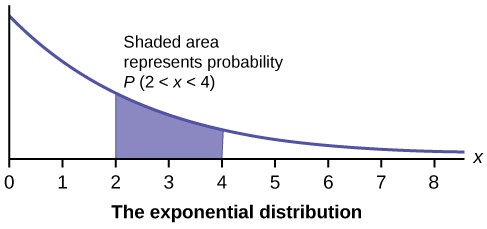
Figure 5.3 The graph shows an Exponential Distribution with the area between x = 2 and x = 4 shaded to represent the probability that the value of the random variable X is in the interval between two and four.

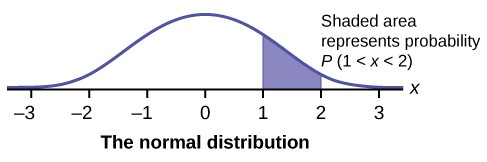
Figure 5.4 The graph shows the Standard Normal Distribution with the area between x = 1 and x = 2 shaded to represent the probability that the value of the random variable X is in the interval between one and two.

For continuous probability distributions, PROBABILITY = AREA.

Example 5.1Consider the function f(x) =for 0 ≤ x ≤ 20. x = a real number. The graph of f(x) =is a horizontal line. 120 120However, since 0 ≤ x ≤ 20, f(x) is restricted to the portion between x = 0 and x = 20, inclusive.Figure 5.5f(x) =for 0 ≤ x ≤ 20. 120

The graph of f(x) = 1

20

is a horizontal line segment when 0 ≤ x ≤ 20.

The area between f(x) = 1

20

where 0 ≤ x ≤ 20 and the x-axis is the area of a rectangle with base = 20 and height

= 1 .

20

⎝20⎠
AREA = 20⎛ 1 ⎞ = 1

Suppose we want to find the area between f(x) = 1

20

and the x-axis where 0 < x < 2.

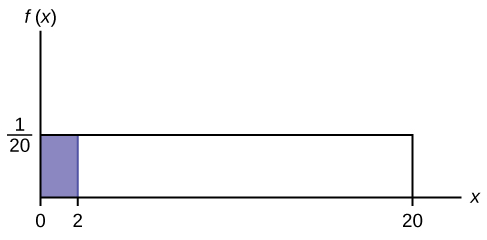
Figure 5.6

⎝20⎠
AREA = (2 – 0)⎛ 1 ⎞ = 0.1

(2 – 0) = 2 = base of a rectangle

REMINDERarea of a rectangle = (base)(height).

The area corresponds to a probability. The probability that x is between zero and two is 0.1, which can be written mathematically as P(0 < x < 2) = P(x < 2) = 0.1.

Suppose we want to find the area between f(x) = 1

20

and the x-axis where 4 < x < 15.

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

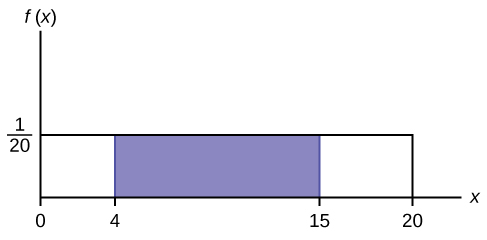
Figure 5.7

⎝20⎠
AREA = (15 – 4)⎛ 1 ⎞ = 0.55

(15 – 4) = 11 = the base of a rectangle

The area corresponds to the probability P(4 < x < 15) = 0.55.

⎝⎠
Suppose we want to find P(x = 15). On an x-y graph, x = 15 is a vertical line. A vertical line has no width (or zero width). Therefore, P(x = 15) = (base)(height) = (0) ⎛ 1 ⎞ = 0

20

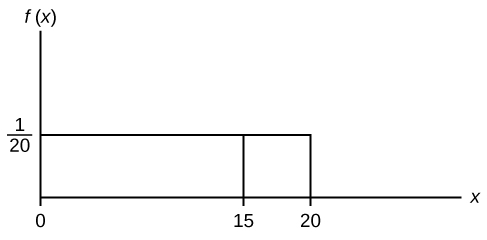
Figure 5.8

P(X ≤ x), which can also be written as P(X < x) for continuous distributions, is called the cumulative distribution function or CDF. Notice the “less than or equal to” symbol. We can also use the CDF to calculate P(X > x). The CDF gives “area to the left” and P(X > x) gives “area to the right.” We calculate P(X > x) for continuous distributions as follows: P(X > x) = 1 – P (X < x).

Figure 5.9

Label the graph with f(x) and x. Scale the x and y axes with the maximum x and y values. f(x) = 1

20

, 0 ≤ x ≤ 20.

To calculate the probability that x is between two values, look at the following graph. Shade the region between x

= 2.3 and x = 12.7. Then calculate the shaded area of a rectangle.

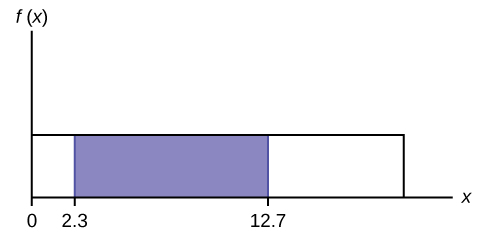
Figure 5.10

⎝20⎠
P(2.3 < x < 12.7) = (base)(height) = (12.7 − 2.3)⎛ 1 ⎞ = 0.52

5.1 Consider the function f(x) =for 0 ≤ x ≤ 8. Draw the graph of f(x) and find P(2.5 < x < 7.5).18

| The Uniform Distribution

The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to occur. When working out problems that have a uniform distribution, be careful to note if the data is inclusive or exclusive of endpoints.

The mathematical statement of the uniform distribution is

−
f(x) =

b 1 a for a ≤ x ≤ b

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

(b − a)212
where a = the lowest value of x and b = the highest value of x. Formulas for the theoretical mean and standard deviation are

5.1 The data that follow are the number of passengers on 35 different charter fishing boats. The sample mean = 7.9 and the sample standard deviation = 4.33. The data follow a uniform distribution where all values between and including zero and 14 are equally likely. State the values of a and b. Write the distribution in proper notation, and calculate the theoretical mean and standard deviation.Table 5.1
2
µ = a + b

and σ =

Example 5.2The amount of time, in minutes, that a person must wait for a bus is uniformly distributed between zero and 15 minutes, inclusive.a. What is the probability that a person waits fewer than 12.5 minutes?Solution 5.2a. Let X = the number of minutes a person must wait for a bus. a = 0 and b = 15. X ~ U(0, 15). Write the probability density function. f (x) =15 1− 015=for 0 ≤ x ≤ 15. 1⎝15⎠The probability a person waits less than 12.5 minutes is 0.8333.Find P (x < 12.5). Draw a graph.P(x < k) = (base)(height) = (12.5 – 0)⎛ 1 ⎞ = 0.8333

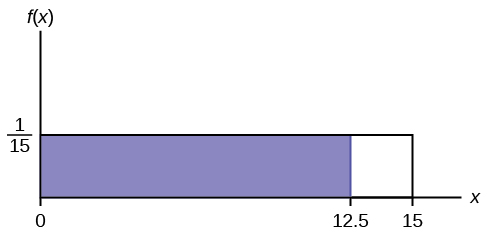
Figure 5.11

b. On the average, how long must a person wait? Find the mean, μ, and the standard deviation, σ.

Solution 5.2

• μ = a + b

2

(b – a)212
σ =

= 15 + 0

2

(15 – 0)212
=

= 7.5. On the average, a person must wait 7.5 minutes.

= 4.3. The Standard deviation is 4.3 minutes.

• NOTEThis asks for the 90th percentile.
  Ninety percent of the time, the time a person must wait falls below what value?

Solution 5.2

c. Find the 90th percentile. Draw a graph. Let k = the 90th percentile.

15
P(x < k) = (base)(height) = (k − 0)( 1 )

⎝15⎠
0.90 = (k)⎛ 1 ⎞

k = (0.90)(15) = 13.5

The 90th percentile is 13.5 minutes. Ninety percent of the time, a person must wait at most 13.5 minutes.

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

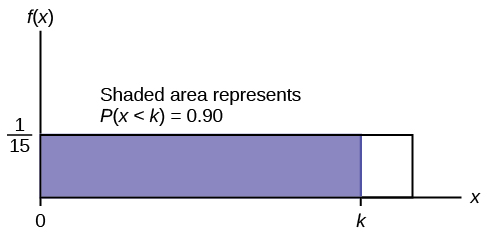
Figure 5.12

5.2 The total duration of baseball games in the major league in the 2011 season is uniformly distributed between 447 hours and 521 hours inclusive.Find a and b and describe what they represent.Write the distribution.Find the mean and the standard deviation.What is the probability that the duration of games for a team for the 2011 season is between 480 and 500 hours?

| The Exponential Distribution

The exponential distribution is often concerned with the amount of time until some specific event occurs. For example, the amount of time (beginning now) until an earthquake occurs has an exponential distribution. Other examples include the length of time, in minutes, of long distance business telephone calls, and the amount of time, in months, a car battery lasts. It can be shown, too, that the value of the change that you have in your pocket or purse approximately follows an exponential distribution.

Values for an exponential random variable occur in the following way. There are fewer large values and more small values. For example, marketing studies have shown that the amount of money customers spend in one trip to the supermarket follows an exponential distribution. There are more people who spend small amounts of money and fewer people who spend large amounts of money.

Exponential distributions are commonly used in calculations of product reliability, or the length of time a product lasts.

The random variable for the exponential distribution is continuous and often measures a passage of time, although it can be used in other applications. Typical questions may be, “what is the probability that some event will occur within the next x hours or days, or what is the probability that some event will occur between x1 hours and x2 hours, or what is the probability that the event will take more than x1 hours to perform?” In short, the random variable X equals (a) the time

between events or (b) the passage of time to complete an action, e.g. wait on a customer. The probability density function is given by:

µ
f (x) = 1 e− 1µ x

where μ is the historical average waiting time. and has a mean and standard deviation of 1/μ.

An alternative form of the exponential distribution formula recognizes what is often called the decay factor. The decay factor simply measures how rapidly the probability of an event declines as the random variable X increases. When the notation using the decay parameter m is used, the probability density function is presented as:

f (x)=me−mx

where m = 1µ

In order to calculate probabilities for specific probability density functions, the cumulative density function is used. The cumulative density function (cdf) is simply the integral of the pdf and is:

⎛ ⎞∞ ⎡

– x ⎤- x

F⎜x⎟ = ∫0⎢1µ e µ ⎥ = 1 – e µ

⎜ ⎟⎢⎥

⎝ ⎠⎣⎦

Example 5.3

Let X = amount of time (in minutes) a postal clerk spends with a customer. The time is known from historical data to have an average amount of time equal to four minutes.

It is given that μ = 4 minutes, that is, the average time the clerk spends with a customer is 4 minutes. Remember that we are still doing probability and thus we have to be told the population parameters such as the mean. To do any calculations, we need to know the mean of the distribution: the historical time to provide a service, for example. Knowing the historical mean allows the calculation of the decay parameter, m.

4
m = 1µ . Therefore, m = 1 = 0.25 .

When the notation used the decay parameter, m, the probability density function is presented as

f (x) = me−mx , which is simply the original formula with m substituted for 1 , or f (x) = 1 e− 1µ x .

µµ

To calculate probabilities for an exponential probability density function, we need to use the cumulative density function. As shown below, the curve for the cumulative density function is:

f(x) = 0.25e–0.25x where x is at least zero and m = 0.25.

For example, f(5) = 0.25e(-0.25)(5) = 0.072. In other words, the function has a value of .072 when x = 5. The graph is as follows:

Figure 5.13

Notice the graph is a declining curve. When x = 0,

f(x) = 0.25e(−0.25)(0) = (0.25)(1) = 0.25 = m. The maximum value on the y-axis is always m, one divided by the

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

mean.

5.3 The amount of time spouses shop for anniversary cards can be modeled by an exponential distribution with the average amount of time equal to eight minutes. Write the distribution, state the probability density function, and graph the distribution.
Example 5.4a. Using the information in Example 5.3, find the probability that a clerk spends four to five minutes with a randomly selected customer.Solution 5.4a. Find P(4 < x < 5).The cumulative distribution function (CDF) gives the area to the left.P(x < x) = 1 – e–mxP(x < 5) = 1 – e(–0.25)(5) = 0.7135 and P(x < 4) = 1 – e(–0.25)(4) = 0.6321P(4 < x < 5)= 0.7135 – 0.6321 = 0.0814Figure 5.14
5.4 The number of days ahead travelers purchase their airline tickets can be modeled by an exponential distribution with the average amount of time equal to 15 days. Find the probability that a traveler will purchase a ticket fewer than ten days in advance. How many days do half of all travelers wait?
Example 5.5On the average, a certain computer part lasts ten years. The length of time the computer part lasts is exponentially distributed.a. What is the probability that a computer part lasts more than 7 years?

Solution 5.5

• Let x = the amount of time (in years) a computer part lasts.

10
μ = 10 so m = 1µ = 1 = 0.1

Find P(x > 7). Draw the graph.

P(x > 7) = 1 – P(x < 7).

Since P(X < x) = 1 – e–mx then P(X > x) = 1 – ( 1 –e–mx) = e–mx

P(x > 7) = e(–0.1)(7) = 0.4966. The probability that a computer part lasts more than seven years is 0.4966.

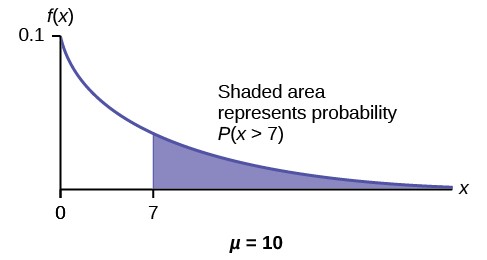
Figure 5.15

• On the average, how long would five computer parts last if they are used one after another?

Solution 5.5

b. On the average, one computer part lasts ten years. Therefore, five computer parts, if they are used one right after the other would last, on the average, (5)(10) = 50 years.

d. What is the probability that a computer part lasts between nine and 11 years?

Solution 5.5

d. Find P(9 < x < 11). Draw the graph.

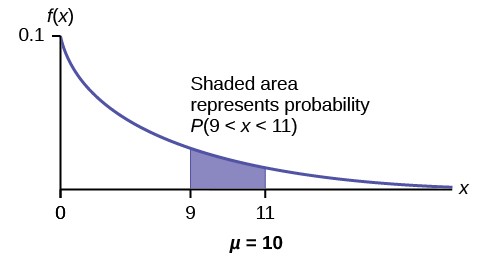
Figure 5.16

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

P(9 < x < 11) = P(x < 11) – P(x < 9) = (1 – e(–0.1)(11)) – (1 – e(–0.1)(9)) = 0.6671 – 0.5934 = 0.0737. The probability

that a computer part lasts between nine and 11 years is 0.0737.

5.5 On average, a pair of running shoes can last 18 months if used every day. The length of time running shoes last is exponentially distributed. What is the probability that a pair of running shoes last more than 15 months? On average, how long would six pairs of running shoes last if they are used one after the other? Eighty percent of running shoes last at most how long if used every day?
Example 5.6Suppose that the length of a phone call, in minutes, is an exponential random variable with decay parameter 112. The decay p[parameter is another way to view 1/λ. If another person arrives at a public telephone just before you, find the probability that you will have to wait more than five minutes. Let X = the length of a phone call, in minutes.What is m, μ, and σ? The probability that you must wait more than five minutes is .Solution 5.6•m = 112• μ = 12• σ = 12P(x > 5) = 0.6592
Example 5.7The time spent waiting between events is often modeled using the exponential distribution. For example, suppose that an average of 30 customers per hour arrive at a store and the time between arrivals is exponentially distributed.On average, how many minutes elapse between two successive arrivals?When the store first opens, how long on average does it take for three customers to arrive?After a customer arrives, find the probability that it takes less than one minute for the next customer to arrive.After a customer arrives, find the probability that it takes more than five minutes for the next customer to arrive.Is an exponential distribution reasonable for this situation?Solution 5.7Since we expect 30 customers to arrive per hour (60 minutes), we expect on average one customer to arrive every two minutes on average.Since one customer arrives every two minutes on average, it will take six minutes on average for three customers to arrive.

c. Let X = the time between arrivals, in minutes. By part a, μ = 2, so m = 1

2

= 0.5.

The cumulative distribution function is P(X < x) = 1 – e(-0.5)(x)

Therefore P(X < 1) = 1 – e(–0.5)(1) = 0.3935.

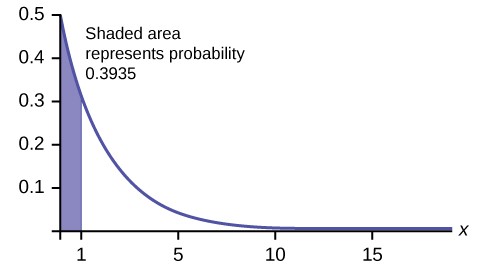
Figure 5.17

d. P(X > 5) = 1 – P(X < 5) = 1 – (1 – e(-0.5)(5)) = e–2.5 ≈ 0.0821.

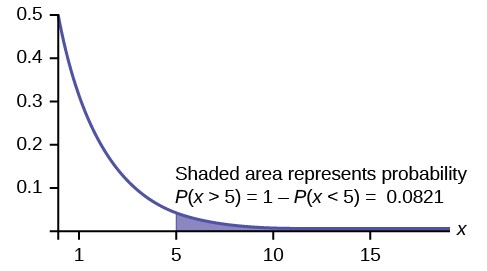
Figure 5.18

e. This model assumes that a single customer arrives at a time, which may not be reasonable since people might shop in groups, leading to several customers arriving at the same time. It also assumes that the flow of customers does not change throughout the day, which is not valid if some times of the day are busier than others.

Memorylessness of the Exponential Distribution

Recall that the amount of time between customers for the postal clerk discussed earlier is exponentially distributed with a mean of two minutes. Suppose that five minutes have elapsed since the last customer arrived. Since an unusually long amount of time has now elapsed, it would seem to be more likely for a customer to arrive within the next minute. With the exponential distribution, this is not the case–the additional time spent waiting for the next customer does not depend on how much time has already elapsed since the last customer. This is referred to as the memoryless property. The exponential and geometric probability density functions are the only probability functions that have the memoryless property. Specifically,

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

the memoryless property says that

P (X > r + t | X > r) = P (X > t) for all r ≥ 0 and t ≥ 0

For example, if five minutes have elapsed since the last customer arrived, then the probability that more than one minute will elapse before the next customer arrives is computed by using r = 5 and t = 1 in the foregoing equation.

P(X > 5 + 1 | X > 5) = P(X > 1) = e( – 0.5)(1) = 0.6065.

This is the same probability as that of waiting more than one minute for a customer to arrive after the previous arrival.

The exponential distribution is often used to model the longevity of an electrical or mechanical device. In Example 5.5, the lifetime of a certain computer part has the exponential distribution with a mean of ten years. The memoryless property says that knowledge of what has occurred in the past has no effect on future probabilities. In this case it means that an old part is not any more likely to break down at any particular time than a brand new part. In other words, the part stays as good as new until it suddenly breaks. For example, if the part has already lasted ten years, then the probability that it lasts another seven years is P(X > 17|X > 10) = P(X > 7) = 0.4966, where the vertical line is read as “given”.

Example 5.8Refer back to the postal clerk again where the time a postal clerk spends with his or her customer has an exponential distribution with a mean of four minutes. Suppose a customer has spent four minutes with a postal clerk. What is the probability that he or she will spend at least an additional three minutes with the postal clerk?The decay parameter of X is m == 0.25, so X ∼ Exp(0.25).4The cumulative distribution function is P(X < x) = 1 – e–0.25x.We want to find P(X > 7|X > 4). The memoryless property says that P(X > 7|X > 4) = P (X > 3), so we just need to find the probability that a customer spends more than three minutes with a postal clerk.This is P(X > 3) = 1 – P (X < 3) = 1 – (1 – e–0.25⋅3) = e–0.75 ≈ 0.4724.1Figure 5.19

Relationship between the Poisson and the Exponential Distribution

There is an interesting relationship between the exponential distribution and the Poisson distribution. Suppose that the time that elapses between two successive events follows the exponential distribution with a mean of μ units of time. Also assume that these times are independent, meaning that the time between events is not affected by the times between previous events.

If these assumptions hold, then the number of events per unit time follows a Poisson distribution with mean μ. Recall that if

µx e− µ

X has the Poisson distribution with mean μ, then P(X = x) =

x !.

µ
The formula for the exponential distribution: P(X = x) = me–mx = 1 e– 1µ x Where m = the rate parameter, or μ = average

time between occurrences.

We see that the exponential is the cousin of the Poisson distribution and they are linked through this formula. There are important differences that make each distribution relevant for different types of probability problems.

First, the Poisson has a discrete random variable, x, where time; a continuous variable is artificially broken into discrete pieces. We saw that the number of occurrences of an event in a given time interval, x, follows the Poisson distribution.

For example, the number of times the telephone rings per hour. By contrast, the time between occurrences follows the exponential distribution. For example. The telephone just rang, how long will it be until it rings again? We are measuring length of time of the interval, a continuous random variable, exponential, not events during an interval, Poisson.

The Exponential Distribution v. the Poisson Distribution

A visual way to show both the similarities and differences between these two distributions is with a time line.

Figure 5.20

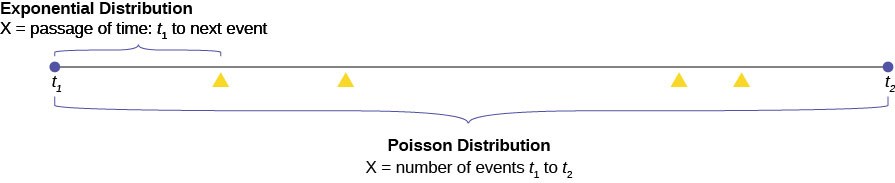
The random variable for the Poisson distribution is discrete and thus counts events during a given time period, t1 to t2 on Figure 5.20, and calculates the probability of that number occurring. The number of events, four in the graph, is measured in counting numbers; therefore, the random variable of the Poisson is a discrete random variable.

The exponential probability distribution calculates probabilities of the passage of time, a continuous random variable. In

Figure 5.20 this is shown as the bracket from t1 to the next occurrence of the event marked with a triangle. Classic Poisson distribution questions are “how many people will arrive at my checkout window in the next hour?”.

Classic exponential distribution questions are “how long it will be until the next person arrives,” or a variant, “how long will the person remain here once they have arrived?”.

Again, the formula for the exponential distribution is:

µ
f (x) = me–mx or f (x) = 1 e– 1µ x

We see immediately the similarity between the exponential formula and the Poisson formula.

x !
P(x) = µx e− µ

Both probability density functions are based upon the relationship between time and exponential growth or decay. The “e” in the formula is a constant with the approximate value of 2.71828 and is the base of the natural logarithmic exponential growth formula. When people say that something has grown exponentially this is what they are talking about.

An example of the exponential and the Poisson will make clear the differences been the two. It will also show the interesting applications they have.

Poisson Distribution

Suppose that historically 10 customers arrive at the checkout lines each hour. Remember that this is still probability so we have to be told these historical values. We see this is a Poisson probability problem.

We can put this information into the Poisson probability density function and get a general formula that will calculate the probability of any specific number of customers arriving in the next hour.

The formula is for any value of the random variable we chose, and so the x is put into the formula. This is the formula:

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

x !
f (x) = 10 x e-10

As an example, the probability of 15 people arriving at the checkout counter in the next hour would be

15 !
P(x = 15) = 1015 e-10 = 0.0611

Here we have inserted x = 15 and calculated the probability that in the next hour 15 people will arrive is .061.

Exponential Distribution

If we keep the same historical facts that 10 customers arrive each hour, but we now are interested in the service time a person spends at the counter, then we would use the exponential distribution. The exponential probability function for any value of x, the random variable, for this particular checkout counter historical data is:

-x

.1
f (x) = 1 e .1 = 10e-10x

To calculate µ, the historical average service time, we simply divide the number of people that arrive per hour, 10 , into the time period, one hour, and have µ = 0.1. Historically, people spend 0.1 of an hour at the checkout counter, or 6 minutes. This explains the .1 in the formula.

There is a natural confusion with µ in both the Poisson and exponential formulas. They have different meanings, although they have the same symbol. The mean of the exponential is one divided by the mean of the Poisson. If you are given the historical number of arrivals you have the mean of the Poisson. If you are given an historical length of time between events you have the mean of an exponential.

Continuing with our example at the checkout clerk; if we wanted to know the probability that a person would spend 9 minutes or less checking out, then we use this formula. First, we convert to the same time units which are parts of one hour. Nine minutes is 0.15 of one hour. Next we note that we are asking for a range of values. This is always the case for a continuous random variable. We write the probability question as:

p⎛x ≤ 9⎞ = 1 – 10e-10x

⎝⎠

We can now put the numbers into the formula and we have our result.

p(x = .15) = 1 – 10e-10(.15) = 0.7769

The probability that a customer will spend 9 minutes or less checking out is 0.7769.

We see that we have a high probability of getting out in less than nine minutes and a tiny probability of having 15 customers arriving in the next hour.

KEY TERMS

Conditional Probability the likelihood that an event will occur given that another event has already occurred.

decay parameter The decay parameter describes the rate at which probabilities decay to zero for increasing values of

x. It is the value m in the probability density function f(x) = me(-mx) of an exponential random variable. It is also equal to m = 1µ , where μ is the mean of the random variable.

Exponential Distribution a continuous random variable (RV) that appears when we are interested in the intervals of time between some random events, for example, the length of time between emergency arrivals at a hospital. The

mean is μ = m1 and the standard deviation is σ = m1 . The probability density function is f (x) = me–mx or

µ
f (x) = 1 e– 1µ x , x ≥ 0 and the cumulative distribution function is P(X ≤ x) = 1 – e−mx or P(X ≤ x) = 1 – e− 1µ x

.

memoryless property For an exponential random variable X, the memoryless property is the statement that knowledge of what has occurred in the past has no effect on future probabilities. This means that the probability that X exceeds x + t, given that it has exceeded x, is the same as the probability that X would exceed t if we had no knowledge about it. In symbols we say that P(X > x + t|X > x) = P(X > t).

Poisson distribution If there is a known average of μ events occurring per unit time, and these events are independent of each other, then the number of events X occurring in one unit of time has the Poisson distribution. The probability

µx e− µ

of x events occurring in one unit time is equal to P(X = x) =

x !.

Uniform Distribution a continuous random variable (RV) that has equally likely outcomes over the domain, a < x < b; it is often referred as the rectangular distribution because the graph of the pdf has the form of a rectangle. The

mean is μ = a + b and the standard deviation is σ = (b − a)2 . The probability density function is f(x) = 1

212b − a

for a < x < b or a ≤ x ≤ b. The cumulative distribution is P(X ≤ x) = x − a .

b − a

CHAPTER REVIEW

Properties of Continuous Probability Density Functions

The probability density function (pdf) is used to describe probabilities for continuous random variables. The area under the density curve between two points corresponds to the probability that the variable falls between those two values. In other words, the area under the density curve between points a and b is equal to P(a < x < b). The cumulative distribution function (cdf) gives the probability as an area. If X is a continuous random variable, the probability density function (pdf), f(x), is used to draw the graph of the probability distribution. The total area under the graph of f(x) is one. The area under the graph of f(x) and between values a and b gives the probability P(a < x < b).

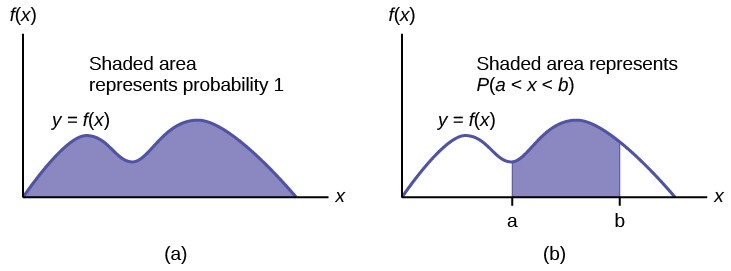
Figure 5.21

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

The cumulative distribution function (cdf) of X is defined by P (X ≤ x). It is a function of x that gives the probability that the random variable is less than or equal to x.

The Uniform Distribution

If X has a uniform distribution where a < x < b or a ≤ x ≤ b, then X takes on values between a and b (may include a and

2
b). All values x are equally likely. We write X ∼ U(a, b). The mean of X is µ = a + b . The standard deviation of X is

σ = (b − a)2 . The probability density function of X is f (x) = 1 for a ≤ x ≤ b. The cumulative distribution function

12

of X is P(X ≤ x) = x − a . X is continuous.

b − a

b − a

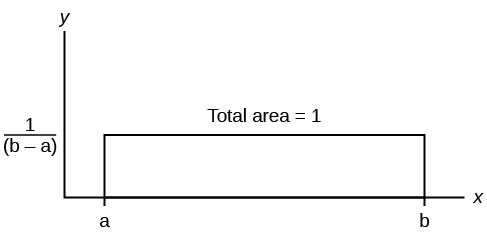
Figure 5.22

The probability P(c < X < d) may be found by computing the area under f(x), between c and d. Since the corresponding area is a rectangle, the area may be found simply by multiplying the width and the height.

The Exponential Distribution

If X has an exponential distribution with mean μ, then the decay parameter is m = 1µ . The probability density function of X is f(x) = me-mx (or equivalently f (x) = 1µ e − x / µ . The cumulative distribution function of X is P(X ≤ x) = 1 – e–mx.

FORMULA REVIEW

PropertiesofContinuousProbability Density Functions

Probability density function (pdf) f(x):

• f(x) ≥ 0

• The total area under the curve f(x) is one. Cumulative distribution function (cdf): P(X ≤ x)

The Uniform Distribution

X = a real number between a and b (in some instances, X

can take on the values a and b). a = smallest X; b = largest

The mean is µ = a + b

(b – a)212
2
The standard deviation is σ =

b − a
Probabilitydensityfunction:f (x) = 1

a ≤ X ≤ b

⎝⎠
Area to the Left of x: P(X < x) = (x – a) ⎛ 1 ⎞

b − a

⎝⎠
Area to the Right of x: P(X > x) = (b – x) ⎛ 1 ⎞

b − a

for

X

X ~ U (a, b)

Area Between c and d: P(c < x < d) = (base)(height) = (d

⎝⎠
– c) ⎛ 1 ⎞

b − a

• b − a
  pdf: f (x) = 1 for a ≤ x ≤ b
• cdf: P(X ≤ x) = x − a

b − a

The Exponential Distribution

• pdf: f(x) = me(–mx) where x ≥ 0 and m > 0

• cdf: P(X ≤ x) = 1 – e(–mx)

• mean µ = m1

• mean µ = a + b

2

• 12
  standard deviation σ = (b − a)2

–
• P(c < X < d) = (d – c) (b 1 a)

PRACTICE

• 
  standard deviation σ = µ
• Additionally

◦ P(X > x) = e(–mx)

◦ P(a < X < b) = e(–ma) – e(–mb)

• Poisson probability: P(X = x) =

and variance of μ

µx e− µ

x !with mean

Properties of Continuous Probability Density Functions

• Which type of distribution does the graph illustrate?

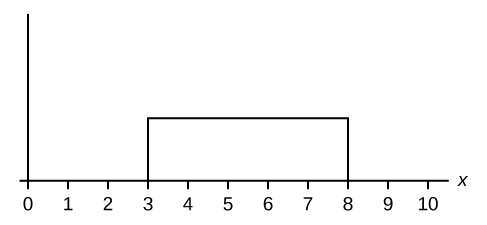
Figure 5.23

• Which type of distribution does the graph illustrate?

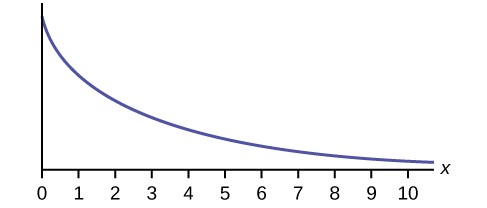
Figure 5.24

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

• Which type of distribution does the graph illustrate?

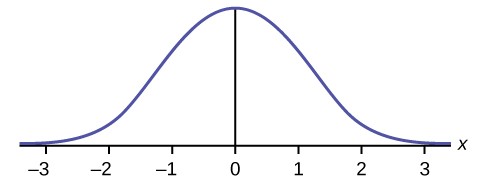
Figure 5.25

• What does the shaded area represent? P( < x < )

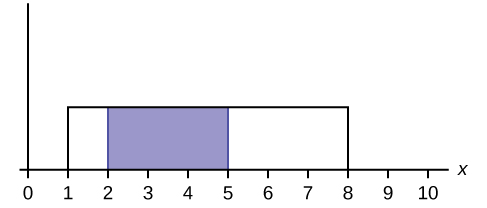
Figure 5.26

• What does the shaded area represent? P( < x < )

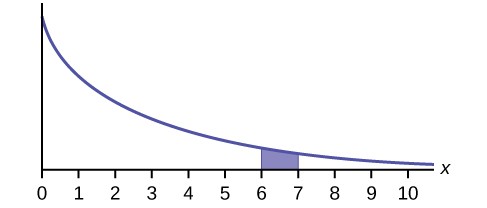
Figure 5.27

• For a continuous probablity distribution, 0 ≤ x ≤ 15. What is P(x > 15)?
• What is the area under f(x) if the function is a continuous probability density function?
• For a continuous probability distribution, 0 ≤ x ≤ 10. What is P(x = 7)?
• A continuous probability function is restricted to the portion between x = 0 and 7. What is P(x = 10)?
• f(x) for a continuous probability function is 1 , and the function is restricted to 0 ≤ x ≤ 5. What is P(x < 0)?

5

• f(x), a continuous probability function, is equal to 1

12

, and the function is restricted to 0 ≤ x ≤ 12. What is P (0 < x <

12)?

• Find the probability that x falls in the shaded area.

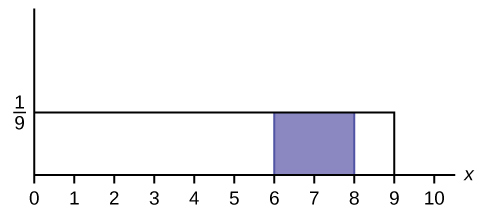
Figure 5.28

• Find the probability that x falls in the shaded area.

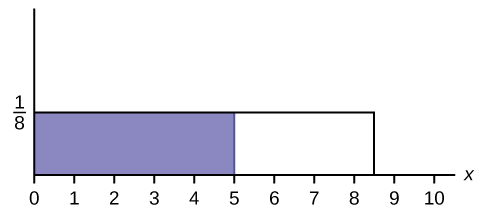
Figure 5.29

• Find the probability that x falls in the shaded area.

Figure 5.30

• f(x), a continuous probability function, is equal to 1

and the function is restricted to 1 ≤ x ≤ 4. Describe P⎛x > 3⎞.

3

• The Uniform Distribution

⎝2⎠

Use the following information to answer the next ten questions. The data that follow are the square footage (in 1,000 feet squared) of 28 homes.

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

Table 5.2

The sample mean = 2.50 and the sample standard deviation = 0.8302. The distribution can be written as X ~ U(1.5, 4.5).

• What type of distribution is this?
• In this distribution, outcomes are equally likely. What does this mean?
• What is the height of f(x) for the continuous probability distribution?
• What are the constraints for the values of x?
• Graph P(2 < x < 3).
• What is P(2 < x < 3)?

22. What is P(x < 3.5 | x < 4)?

• What is P(x = 1.5)?
• Find the probability that a randomly selected home has more than 3,000 square feet given that you already know the house has more than 2,000 square feet.

Use the following information to answer the next eight exercises. A distribution is given as X ~ U(0, 12).

• What is a? What does it represent?
• What is b? What does it represent?
• What is the probability density function?
• What is the theoretical mean?
• What is the theoretical standard deviation?
• Draw the graph of the distribution for P(x > 9).
• Find P(x > 9).

Use the following information to answer the next eleven exercises. The age of cars in the staff parking lot of a suburban college is uniformly distributed from six months (0.5 years) to 9.5 years.

• What is being measured here?
• In words, define the random variable X.
• Are the data discrete or continuous?
• The interval of values for x is .
• The distribution for X is .
• Write the probability density function.

• Graph the probability distribution.
• Sketch the graph of the probability distribution.

Figure 5.31

• –
  Identify the following values:
• Lowest value for x :
• Highest value for –x :
• Height of the rectangle:
• Label for x-axis (words):
• Label for y-axis (words):
• Find the average age of the cars in the lot.
• Find the probability that a randomly chosen car in the lot was less than four years old.
• Sketch the graph, and shade the area of interest.

Figure 5.32

• Find the probability. P(x < 4) =

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

• Considering only the cars less than 7.5 years old, find the probability that a randomly chosen car in the lot was less than four years old.
• Sketch the graph, shade the area of interest.

Figure 5.33

• Find the probability. P(x < 4 | x < 7.5) =
• What has changed in the previous two problems that made the solutions different?
• Find the third quartile of ages of cars in the lot. This means you will have to find the value such that 3 , or 75%, of the

4

cars are at most (less than or equal to) that age.

• Sketch the graph, and shade the area of interest.

Figure 5.34

• Find the value k such that P(x < k) = 0.75.
• The third quartile is

The Exponential Distribution

Use the following information to answer the next ten exercises. A customer service representative must spend different amounts of time with each customer to resolve various concerns. The amount of time spent with each customer can be modeled by the following distribution: X ~ Exp(0.2)

• What type of distribution is this?
• Are outcomes equally likely in this distribution? Why or why not?
• What is m? What does it represent?
• What is the mean?
• What is the standard deviation?

• State the probability density function.
• Graph the distribution.

51. Find P(2 < x < 10).

• Find P(x > 6).
• Find the 70th percentile.

Use the following information to answer the next seven exercises. A distribution is given as X ~ Exp(0.75).

• What is m?
• What is the probability density function?
• What is the cumulative distribution function?
• Draw the distribution.
• Find P(x < 4).
• Find the 30th percentile.
• Find the median.
• Which is larger, the mean or the median?

Use the following information to answer the next 16 exercises. Carbon-14 is a radioactive element with a half-life of about 5,730 years. Carbon-14 is said to decay exponentially. The decay rate is 0.000121. We start with one gram of carbon-14. We are interested in the time (years) it takes to decay carbon-14.

• What is being measured here?
• Are the data discrete or continuous?
• In words, define the random variable X.
• What is the decay rate (m)?
• The distribution for X is .
• Find the amount (percent of one gram) of carbon-14 lasting less than 5,730 years. This means, find P(x < 5,730).
• Sketch the graph, and shade the area of interest.

Figure 5.35

• Find the probability. P(x < 5,730) =

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

• Find the percentage of carbon-14 lasting longer than 10,000 years.
• Sketch the graph, and shade the area of interest.

Figure 5.36

• Find the probability. P(x > 10,000) =
• Thirty percent (30%) of carbon-14 will decay within how many years?
• Sketch the graph, and shade the area of interest.

Figure 5.37

• Find the value k such that P(x < k) = 0.30.

HOMEWORK

Properties of Continuous Probability Density Functions

For each probability and percentile problem, draw the picture.

• Consider the following experiment. You are one of 100 people enlisted to take part in a study to determine the percent of nurses in America with an R.N. (registered nurse) degree. You ask nurses if they have an R.N. degree. The nurses answer “yes” or “no.” You then calculate the percentage of nurses with an R.N. degree. You give that percentage to your supervisor.
• What part of the experiment will yield discrete data?
• What part of the experiment will yield continuous data?
• When age is rounded to the nearest year, do the data stay continuous, or do they become discrete? Why?

The Uniform Distribution

For each probability and percentile problem, draw the picture.

• Births are approximately uniformly distributed between the 52 weeks of the year. They can be said to follow a uniform distribution from one to 53 (spread of 52 weeks).
• Graph the probability distribution.
• f(x) = c. μ= d. σ =

e. Find the probability that a person is born at the exact moment week 19 starts. That is, find P(x = 19) =

f. P(2 < x < 31) =

g. Find the probability that a person is born after week 40. h. P(12 < x | x < 28) =

• A random number generator picks a number from one to nine in a uniform manner.
• Graph the probability distribution.
• f(x) = c. μ = d. σ=

e. P(3.5 < x < 7.25) =

f. P(x > 5.67)

g. P(x > 5 | x > 3) =

• According to a study by Dr. John McDougall of his live-in weight loss program at St. Helena Hospital, the people who follow his program lose between six and 15 pounds a month until they approach trim body weight. Let’s suppose that the weight loss is uniformly distributed. We are interested in the weight loss of a randomly selected individual following the program for one month.
• Define the random variable. X =
• Graph the probability distribution.
• f(x) = d. μ = e. σ =
• Find the probability that the individual lost more than ten pounds in a month.
• Suppose it is known that the individual lost more than ten pounds in a month. Find the probability that he lost less than 12 pounds in the month.
• P(7 < x < 13 | x > 9) = . State this in a probability question, similarly to parts g and h, draw the

picture, and find the probability.

• A subway train on the Red Line arrives every eight minutes during rush hour. We are interested in the length of time a commuter must wait for a train to arrive. The time follows a uniform distribution.
• Define the random variable. X =
• Graph the probability distribution.
• f(x) = d. μ = e. σ =
• Find the probability that the commuter waits less than one minute.
• Find the probability that the commuter waits between three and four minutes.
• The age of a first grader on September 1 at Garden Elementary School is uniformly distributed from 5.8 to 6.8 years. We randomly select one first grader from the class.
• Define the random variable. X =
• Graph the probability distribution.
• f(x) = d. μ = e. σ =
• Find the probability that she is over 6.5 years old.
• Find the probability that she is between four and six years old.

Use the following information to answer the next three exercises. The Sky Train from the terminal to the rental–car and

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

long–term parking center is supposed to arrive every eight minutes. The waiting times for the train are known to follow a uniform distribution.

• What is the average waiting time (in minutes)?
• zero
• two
• three
• four
• The probability of waiting more than seven minutes given a person has waited more than four minutes is? a. 0.125

b. 0.25

c. 0.5

d. 0.75

• The time (in minutes) until the next bus departs a major bus depot follows a distribution with f(x) = 1

20

where x goes

from 25 to 45 minutes.

• Define the random variable. X =
• Graph the probability distribution.
• The distribution is (name of distribution). It is (discrete or continuous). d. μ =

e. σ =

• Find the probability that the time is at most 30 minutes. Sketch and label a graph of the distribution. Shade the area of interest. Write the answer in a probability statement.
• Find the probability that the time is between 30 and 40 minutes. Sketch and label a graph of the distribution. Shade the area of interest. Write the answer in a probability statement.
• P(25 < x < 55) = . State this in a probability statement, similarly to parts g and h, draw the picture, and find the probability.
• Suppose that the value of a stock varies each day from $16 to $25 with a uniform distribution.
• Find the probability that the value of the stock is more than $19.
• Find the probability that the value of the stock is between $19 and $22.
• Given that the stock is greater than $18, find the probability that the stock is more than $21.
• A fireworks show is designed so that the time between fireworks is between one and five seconds, and follows a uniform distribution.
• Find the average time between fireworks.
• Find probability that the time between fireworks is greater than four seconds.
• The number of miles driven by a truck driver falls between 300 and 700, and follows a uniform distribution.
• Find the probability that the truck driver goes more than 650 miles in a day.
• Find the probability that the truck drivers goes between 400 and 650 miles in a day.

The Exponential Distribution

• Suppose that the length of long distance phone calls, measured in minutes, is known to have an exponential distribution with the average length of a call equal to eight minutes.
• Define the random variable. X = .
• Is X continuous or discrete? c. μ =

d. σ =

• Draw a graph of the probability distribution. Label the axes.
• Find the probability that a phone call lasts less than nine minutes.
• Find the probability that a phone call lasts more than nine minutes.
• Find the probability that a phone call lasts between seven and nine minutes.
• If 25 phone calls are made one after another, on average, what would you expect the total to be? Why?

• Suppose that the useful life of a particular car battery, measured in months, decays with parameter 0.025. We are interested in the life of the battery.
• Define the random variable. X = .
• Is X continuous or discrete?
• On average, how long would you expect one car battery to last?
• On average, how long would you expect nine car batteries to last, if they are used one after another?
• Find the probability that a car battery lasts more than 36 months.
• Seventy percent of the batteries last at least how long?
• The percent of persons (ages five and older) in each state who speak a language at home other than English is approximately exponentially distributed with a mean of 9.848. Suppose we randomly pick a state.
• Define the random variable. X = .
• Is X continuous or discrete? c. μ =

d. σ =

• Draw a graph of the probability distribution. Label the axes.
• Find the probability that the percent is less than 12.
• Find the probability that the percent is between eight and 14.
• The percent of all individuals living in the United States who speak a language at home other than English is 13.8.

• Why is this number different from 9.848%?
• What would make this number higher than 9.848%?
• The time (in years) after reaching age 60 that it takes an individual to retire is approximately exponentially distributed with a mean of about five years. Suppose we randomly pick one retired individual. We are interested in the time after age 60 to retirement.
• Define the random variable. X = .
• Is X continuous or discrete? c. μ =

d. σ =

• Draw a graph of the probability distribution. Label the axes.
• Find the probability that the person retired after age 70.
• Do more people retire before age 65 or after age 65?
• In a room of 1,000 people over age 80, how many do you expect will NOT have retired yet?
• The cost of all maintenance for a car during its first year is approximately exponentially distributed with a mean of

$150.

• Define the random variable. X = . b. μ =

c. σ =

• Draw a graph of the probability distribution. Label the axes.
• Find the probability that a car required over $300 for maintenance during its first year.

Use the following information to answer the next three exercises. The average lifetime of a certain new cell phone is three years. The manufacturer will replace any cell phone failing within two years of the date of purchase. The lifetime of these cell phones is known to follow an exponential distribution.

• The decay rate is: a. 0.3333

b. 0.5000

• 2
• 3
• What is the probability that a phone will fail within two years of the date of purchase? a. 0.8647

b. 0.4866

c. 0.2212

d. 0.9997

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

• What is the median lifetime of these phones (in years)? a. 0.1941

b. 1.3863

c. 2.0794

d. 5.5452

• At a 911 call center, calls come in at an average rate of one call every two minutes. Assume that the time that elapses from one call to the next has the exponential distribution.
• On average, how much time occurs between five consecutive calls?
• Find the probability that after a call is received, it takes more than three minutes for the next call to occur.
• Ninety-percent of all calls occur within how many minutes of the previous call?
• Suppose that two minutes have elapsed since the last call. Find the probability that the next call will occur within the next minute.
• Find the probability that less than 20 calls occur within an hour.
• In major league baseball, a no-hitter is a game in which a pitcher, or pitchers, doesn’t give up any hits throughout the game. No-hitters occur at a rate of about three per season. Assume that the duration of time between no-hitters is exponential.
• What is the probability that an entire season elapses with a single no-hitter?
• If an entire season elapses without any no-hitters, what is the probability that there are no no-hitters in the following season?
• What is the probability that there are more than 3 no-hitters in a single season?
• During the years 1998–2012, a total of 29 earthquakes of magnitude greater than 6.5 have occurred in Papua New Guinea. Assume that the time spent waiting between earthquakes is exponential.
• What is the probability that the next earthquake occurs within the next three months?
• Given that six months has passed without an earthquake in Papua New Guinea, what is the probability that the next three months will be free of earthquakes?
• What is the probability of zero earthquakes occurring in 2014?
• What is the probability that at least two earthquakes will occur in 2014?
• According to the American Red Cross, about one out of nine people in the U.S. have Type B blood. Suppose the blood types of people arriving at a blood drive are independent. In this case, the number of Type B blood types that arrive roughly follows the Poisson distribution.
• If 100 people arrive, how many on average would be expected to have Type B blood?
• What is the probability that over 10 people out of these 100 have type B blood?
• What is the probability that more than 20 people arrive before a person with type B blood is found?
• A web site experiences traffic during normal working hours at a rate of 12 visits per hour. Assume that the duration between visits has the exponential distribution.
• Find the probability that the duration between two successive visits to the web site is more than ten minutes.
• The top 25% of durations between visits are at least how long?
• Suppose that 20 minutes have passed since the last visit to the web site. What is the probability that the next visit will occur within the next 5 minutes?
• Find the probability that less than 7 visits occur within a one-hour period.
• At an urgent care facility, patients arrive at an average rate of one patient every seven minutes. Assume that the duration between arrivals is exponentially distributed.
• Find the probability that the time between two successive visits to the urgent care facility is less than 2 minutes.
• Find the probability that the time between two successive visits to the urgent care facility is more than 15 minutes.
• If 10 minutes have passed since the last arrival, what is the probability that the next person will arrive within the next five minutes?
• Find the probability that more than eight patients arrive during a half-hour period.

REFERENCES

The Uniform Distribution

McDougall, John A. The McDougall Program for Maximum Weight Loss. Plume, 1995.

The Exponential Distribution

Data from the United States Census Bureau.

Data from World Earthquakes, 2013. Available online at http://www.world-earthquakes.com/ (accessed June 11, 2013).

“No-hitter.” Baseball-Reference.com, 2013. Available online at http://www.baseball-reference.com/bullpen/No-hitter (accessed June 11, 2013).

Zhou, Rick. “Exponential Distribution lecture slides.” Available online at www.public.iastate.edu/~riczw/stat330s11/ lecture/lec13.pdf (accessed June 11, 2013).

SOLUTIONS

1 Uniform Distribution

3 Normal Distribution

5 P(6 < x < 7)

7 one

9 zero

11 one

13 0.625

15 The probability is equal to the area from x = 3

2

to x = 4 above the x-axis and up to f(x) = 1 .

3

17 It means that the value of x is just as likely to be any number between 1.5 and 4.5.

19 1.5 ≤ x ≤ 4.5

21 0.3333

23 zero

24 0.6

26 b is 12, and it represents the highest value of x.

28 six

30

Figure 5.38

33 X = The age (in years) of cars in the staff parking lot

35 0.5 to 9.5

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

37 f(x) = 1

9

where x is between 0.5 and 9.5, inclusive.

39 μ = 5

41

• Check student’s solution.

b.3.5

7

43

a. Check student’s solution. b. k = 7.25

c. 7.25

45 No, outcomes are not equally likely. In this distribution, more people require a little bit of time, and fewer people require a lot of time, so it is more likely that someone will require less time.

47 five

49 f(x) = 0.2e-0.2x

51 0.5350

53 6.02

55 f(x) = 0.75e-0.75x

57

Figure 5.39

59 0.4756

0.75
61 The mean is larger. The mean is

63 continuous 65 m = 0.000121 67

• Check student’s solution

b. P(x < 5,730) = 0.5001

69

a. Check student’s solution. b. k = 2947.73

m1 = 1 ≈ 1.33 , which is greater than 0.9242.

71 Age is a measurement, regardless of the accuracy used.

73

• Check student’s solution.

• 8
  f (x) = 1

where 1 ≤ x ≤ 9

• five

d. 2.3

e.15 32

f.333

800

g.2 3

75

• X represents the length of time a commuter must wait for a train to arrive on the Red Line.
• Graph the probability distribution.

• 8
  f (x) = 1

where 0 ≤ x ≤ 8

• four

e. 2.31

1

8

• 1 8

• d
• b

80

• The probability density function of X is 1= 1 .

P(X > 19) = (25 – 19) ⎛1⎞ = 6 = 2 .

25 − 169

⎝9⎠93

Figure 5.40

b. P(19 < X < 22) = (22 – 19) ⎛1⎞ = 3 = 1 .

⎝9⎠93

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

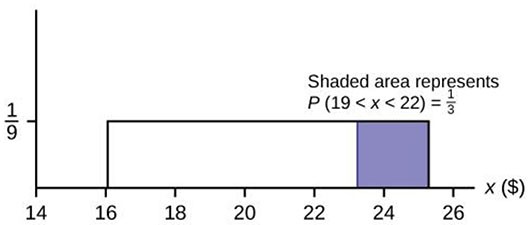
Figure 5.41

• This is a conditional probability question. P(x > 21 | x > 18). You can do this two ways:
• Draw the graph where a is now 18 and b is still 25. The height is 1= 1

⎝7⎠
So, P(x > 21 | x > 18) = (25 – 21) ⎛1⎞ = 4/7.

P(x > 18)
◦ Use the formula: P(x > 21 | x > 18) = P(x > 21 ∩ x > 18)

(25 − 18)7

= P(x > 21)

P(x > 18)

= (25 − 21)

(25 − 18)

= 4 .

7

82

a. P(X > 650) = 700 − 650 = 50 = 1 = 0.125.

700 − 3004008

b. P(400 < X < 650) = 650 − 400 = 250

= 0.625

700 − 300400

84

• X = the useful life of a particular car battery, measured in months.
• X is continuous.
• 40 months
• 360 months e. 0.4066

f. 14.27

86

• X = the time (in years) after reaching age 60 that it takes an individual to retire
• X is continuous.
• five
• five
• Check student’s solution. f. 0.1353

g. before

h. 18.3

88 a

90 c

92 Let X = the number of no-hitters throughout a season. Since the duration of time between no-hitters is exponential, the number of no-hitters per season is Poisson with mean λ = 3.

Therefore, (X = 0) = 30 e – 3

0!

= e–3 ≈ 0.0498

NOTEYou could let T = duration of time between no-hitters. Since the time is exponential and there are 3 no-hitters perseason, then the time between no-hitters is 1 season. For the exponential, µ = 1 .33Therefore, m = 1µ = 3 and T ∼ Exp(3).

• The desired probability is P(T > 1) = 1 – P(T < 1) = 1 – (1 – e–3) = e–3 ≈ 0.0498.
• Let T = duration of time between no-hitters. We find P(T > 2|T > 1), and by the memoryless property this is simply

P(T > 1), which we found to be 0.0498 in part a.

• Let X = the number of no-hitters is a season. Assume that X is Poisson with mean λ = 3. Then P(X > 3) = 1 – P(X ≤ 3)

= 0.3528.

94

a.100

9

= 11.11

b. P(X > 10) = 1 – P(X ≤ 10) = 1 – Poissoncdf(11.11, 10) ≈ 0.5532.

• The number of people with Type B blood encountered roughly follows the Poisson distribution, so the number of people X who arrive between successive Type B arrivals is roughly exponential with mean μ = 9 and m = 1

9

. The cumulative distribution function of X is P(X < x) = 1 − e

− x

9 . Thus hus, P(X > 20) = 1 – P(X ≤ 20) =

⎛

⎝
1 − ⎜1 − e

− 20⎞

9 ⎟ ≈ 0.1084.
⎠

NOTEWe could also deduce that each person arriving has a 8/9 chance of not having Type B blood. So the probabilitythat none of the first 20 people arrive have Type B blood is ⎛8⎞20 ≈ 0.0948 . (The geometric distribution is⎝9⎠more appropriate than the exponential because the number of people between Type B people is discrete instead of continuous.)

96 Let T = duration (in minutes) between successive visits. Since patients arrive at a rate of one patient every seven

t

7
minutes, μ = 7 and the decay constant is m = 1 . The cdf is P(T < t) = 1 − e 7

a. P(T < 2) = 1 – 1 − e

− 2

7 ≈ 0.2485.

⎛

− 15⎞

− 15

⎝
⎠
b. P(T > 15) = 1 − P(T < 15) = 1 − ⎜1 − e

7 ⎟ ≈ e

7 ≈ 0.1173 .

⎛

⎝
c. P(T > 15|T > 10) = P(T > 5) = 1 − ⎜1 − e

− 5⎞

7⎟ = e
⎠

− 5

7 ≈ 0.4895 .

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33

• Let X = # of patients arriving during a half-hour period. Then X has the Poisson distribution with a mean of 30 , X ∼

7

⎝⎠
Poisson ⎛30⎞ . Find P(X > 8) = 1 – P(X ≤ 8) ≈ 0.0311.

7

This OpenStax book is available for free at http://cnx.org/content/col11776/1.33