VI. Jazz
79
John Kocur
Key Takeaways
Chord-Scale Theory is an approach to improvising that relates chords to scales.
- The name "Chord-Scale Theory" comes from the idea that the notes of a thirteenth chord can be rearranged as a seven-note scale.
- To determine chord-scales, identify key centers and chord functions through Roman numeral analysis.
- Roman numerals can be related to mode numbers. For example, if a chord is a ii chord in a major key, the second mode (dorian) can be used to color that chord.
- When playing chord-scales, place chord tones on the downbeat to connect improvised melodies to the chord progression.
This book covers modes from many different angles. For more information on modes, check Introduction to Diatonic Modes (general), Modal Schemas (pop), Diatonic Modes (20th/21st-c.), and Analyzing with Modes, Scales, and Collections (20th-/21st-c.).
One of the challenges of improvising jazz is making choices about pitches while also paying attention to groove, interaction, and narrative form. The Chord-Scale Theory is a method, taught at the Berklee College of Music and many other colleges and universities, that facilitates pitch choices in jazz improvisation. Chord-Scale Theory is based on George Russell’s Lydian Chromatic Concept of Tonal Organization ([1953] 2001), and it was popularized by jazz educators Jamey Aebersold, David Baker, and Jerry Coker.
The basic concept is that every chord comes from a parent scale; or, to put it another way, every chord in a progression can be colored by a related scale. For example, a Dmi7 chord extended to the thirteenth consists of the notes D, F, A, C, E, G, and B, which are identical to the notes of the D dorian mode stacked in thirds (Example 1). Therefore, when confronting a Dmi7 chord in a chord progression, an improvising musician could choose to improvise using the notes of the D dorian mode to create new melodies.
https://musescore.com/user/32728834/scores/6300405/embed
Example 1. A Dmi13 chord and a D dorian scale have identical pitches.
Basic Chord-Scale Relationships
Starting a major scale on each of its seven notes will yield seven different modes. Each of the modes will have a different pattern of half steps and whole steps and thus a different color. (For more information, see Introduction to Diatonic Modes and/or Diatonic Modes).
Since the ii–V–I schema is so common in jazz standards, the three chord-scale relationships in Example 2 are often taught first. Example 3 shows these three relationships within the context of a ii–V–I progression in C.
[table “49” not found /]
Example 2. Basic chord-scale relationships.
https://musescore.com/user/32728834/scores/6300394/embed
Example 3. Chord-scale relationships in a ii–V–I progression in C.
A beginning improviser might approach a song consisting mainly of ii–V–I progressions by simply applying the dorian mode to minor seventh chords, the mixolydian mode to dominant seventh chords, and the ionian mode to major seventh chords. As Example 4 shows, an improvised melody can imply a harmony by placing chord tones on the downbeats, and a seven-note mode can be thought of as a four-note seventh chord with three passing tones [latex](\hat{2}[/latex], [latex]\hat{4}[/latex], [latex]\hat{6})[/latex] or extensions (ninth, eleventh, thirteenth).
https://musescore.com/user/32728834/scores/6300392/embed
Example 4. The basic chord-scale relationships for ii–V–I as they might be used in "Tune Up" by Miles Davis (1953).
Chord-Scales and Major Keys
There are many more possible chord-scale relationships beyond those above. The seven notes of the diatonic scale suggest seven basic chord-scale relationships, as summarized in Examples 5 and 6.
[table “50” not found /]
Example 5. Chord-scale relationships between Roman numerals and modes.
https://musescore.com/user/32728834/scores/6300399/embed
Example 6. Chord-scale relationships for all diatonic harmonies in C.
A similar approach to the one above can be used to derive more chord-scale relationships from the melodic minor, harmonic minor, and harmonic major modes. To learn more about this, consult Further Reading below.
Applying Chord-Scales to Progressions within a Key
Reorganizing these relationships by chord quality reveals the choices listed in Example 7 for matching chord qualities to scales. For example, when improvising on a minor seventh chord, a musician can choose from three chord-scales: dorian, phrygian, or aeolian (Example 8).
[table “51” not found /]
Example 7. The same chord-scale relationships as in Example 5, rearranged by chord quality.
https://musescore.com/user/32728834/scores/6300396/embed
Example 8. Chord-scale choices for a minor-seventh chord.
However, it's important to realize that Chord-Scale Theory does not imply that the key modulates each time the chord changes. In other words, these chord-scales are not key centers. Since each mode will imply different extensions, identifying chord functions through Roman numeral analysis helps an improviser choose chord-scales that best fit the key center.
For example, the opening measures of “Fly Me to the Moon” (1954) contain six of the seven diatonic chord-scale relationships in a circle-of-fifths root movement (Example 9). The chord progression in this example is clearly in the key of C, not seven different keys. Rather than simply coloring each minor chord with a dorian mode and each major chord with an ionian mode, differentiating between the vi and ii chords and between the I and IV chords will result in a more natural-sounding improvised line.
https://musescore.com/user/32728834/scores/6301594/embed
Example 9. These chord-scales applied to "Fly Me to the Moon" by Bart Howard (1954) distinguish between different chords of the same quality, because the chords still have different functions.
Example 10 is the a transcription of the first chorus of John Coltrane’s improvised solo on “Giant Steps" (1960), transposed to B♭ for tenor saxophone. Because of the fast tempo and unusual key center relationships, Coltrane improvises melodies that consist mainly of arpeggios and scale fragments. Note how he uses the ionian mode on major chords, the mixolydian mode (with a passing tone between do and te [[latex]\hat{1}[/latex] and [latex]\downarrow\hat{7}[/latex]] in m. 9) on dominant seventh chords, and the dorian mode on minor chords.
https://musescore.com/user/32728834/scores/6300401/embed
Example 10. Transcription of the first chorus of “Giant Steps" by John Coltrane (1960).
Limitations of Chord-Scale Theory
Some jazz educators have pointed out limitations of the Chord-Scale approach, such as:
- The absence of voice leading between chords. Chord-Scale Theory can lead a student to see each chord as a new key center, instead of viewing an entire chord progression as derived from a parent scale. This can result in choppy, un-melodic improvisation that lacks smooth voice leading between chords.
- Lack of the chromaticism commonly used in bebop and blues-based styles. Chord-Scale Theory generally does not account for neighbor tones, passing tones, secondary leading tones, and blue notes employed by bebop musicians such as Charlie Parker, Dizzy Gillespie, and Bud Powell.
- The anachronism of applying a 1960s modal concept to tunes from 1920–50. Louis Armstrong and Charlie Parker did not think in terms of chord-scales. Educators such as Hal Galper and Hal Crook emphasize the importance of melodic embellishment, chord tone improvisation, and blues-based improvisation before delving into chord-scale relationships.
- The avoidance of the oral tradition. Chord-Scale Theory emphasizes the eye and intellect rather than the ear and intuition. Practicing chord-scale relationships does not substitute for transcribing improvised jazz solos, memorizing tunes, improvising along with recordings, or jamming with other musicians as the preferred methods of learning the oral tradition of jazz improvisation.
- Haerle, Dan. 1982. The Jazz Language: A Theory Text for Jazz Composition and Improvisation. Hialeah, FL: Alfred Music.
- Nettles, Barrie, and Richard Graf. 2015. The Chord Scale Theory & Jazz Harmony. Mainz: Alfred Music.
- Russell, George. (1953) 2001. The Lydian Chromatic Concept of Tonal Organization: The Art and Science of Tonal Gravity by George Russell. 4th edition. Brookline, MA: Concept Publishing Company.
- Coming soon!
The role that a musical element plays in the creation of a larger musical unit.
A diatonic mode that follows the pattern W–H–W–W–W–H–W. This is like the natural minor scale, but with a raised 6̂. This scale can also be found by playing the white notes of the piano starting on D.
.front-matter h6 {
font-size: 1.25em;
}
.textbox--sidebar {
float: right;
margin: 1em 0 1em 1em;
max-width: 45%;
}
.textbox.textbox--key-takeaways .textbox__header p {
font: sans-serif !important;
font-weight: bold;
text-transform: uppercase;
font-style: normal;
font-size: larger;
}
.a.button {
text-decoration: none;
}
Key Takeaways
In Western musical notation, pitches are designated by the first seven letters of the Latin alphabet: A, B, C, D, E, F, and G. After G these letter names repeat in a loop: A, B, C, D, E, F, G, A, B, C, D, E, F, G, A, B, C, etc. This loop of letter names exists because musicians and music theorists today accept what is called octave equivalence, or the assumption that pitches separated by an octave should have the same letter name. More information about this concept can be found in the next chapter, The Keyboard and the Grand Staff.
This assumption varies with milieu. For example, some ancient Greek music theorists did not accept octave equivalence. These theorists used more than seven letters of the Greek alphabet to name pitches.
Clefs and Ranges
The Notation of Notes, Clefs, and Ledger Lines chapter introduced four clefs: treble, bass, alto, and tenor. A clef indicates which pitches are assigned to the lines and spaces on a staff. In the next chapter, The Keyboard and the Grand Staff, we will see that having multiple clefs makes reading different ranges easier. The treble clef is typically used for higher voices and instruments, such as a flute, violin, trumpet, or soprano voice. The bass clef is usually utilized for lower voices and instruments, such as a bassoon, cello, trombone, or bass voice. The alto clef is primarily used for the viola, a mid-ranged instrument, while the tenor clef is sometimes employed in cello, bassoon, and trombone music (although the principal clef used for these instruments is the bass clef).
Each clef indicates how the lines and spaces of the staff correspond to pitch. Memorizing the patterns for each clef will help you read music written for different voices and instruments.
Reading Treble Clef
The treble clef is one of the most commonly used clefs today. Example 1 shows the letter names used for the lines of a staff when a treble clef is employed. One mnemonic device that may help you remember this order of letter names is "Every Good Bird Does Fly" (E, G, B, D, F). As seen in Example 1, the treble clef wraps around the G line (the second line from the bottom). For this reason, it is sometimes called the "G clef."

Example 2 shows the letter names used for the spaces of a staff with a treble clef. Remembering that these letter names spell the word "face" may make identifying these spaces easier.

Reading Bass Clef
The other most commonly used clef today is the bass clef. Example 3 shows the letter names used for the lines of a staff when a bass clef is employed. A mnemonic device for this order of letter names is “Good Bikes Don’t Fall Apart” (G, B, D, F, A). The bass clef is sometimes called the “F clef”; as seen in Example 3, the dot of the bass clef begins on the F line (the second line from the top).

Example 4 shows the letter names used for the spaces of a staff with a bass clef. The mnemonic device "All Cows Eat Grass" (A, C, E, G) may make identifying these spaces easier.

Reading Alto Clef
Example 5 shows the letter names used for the lines of the staff with the alto clef, which is less commonly used today. The mnemonic device “Fat Alley Cats Eat Garbage” (F, A, C, E, G) may help you remember this order of letter names. As seen in Example 5, the center of the alto clef is indented around the C line (the middle line). For this reason it is sometimes called a "C clef."

Example 6 shows the letter names used for the spaces of a staff with an alto clef, which can be remembered with the mnemonic device “Grand Boats Drift Flamboyantly” (G, B, D, F).

Reading Tenor Clef
The tenor clef, another less commonly used clef, is also sometimes called a “C clef,” but the center of the clef is indented around the second line from the top. Example 7 shows the letter names used for the lines of a staff when a tenor clef is employed, which can be remembered with the mnemonic device “Dodges, Fords, and Chevrolets Everywhere” (D, F, A, C, E):

Example 8 shows the letter names used for the spaces of a staff with a tenor clef. The mnemonic device "Elvis's Guitar Broke Down" (E, G, B, D) may make identifying these spaces easier.

Ledger Lines
When notes are too high or low to be written on a staff, small lines are drawn to extend the staff. You may recall from the previous chapter that these extra lines are called ledger lines. Ledger lines can be used to extend a staff with any clef. Example 9 shows ledger lines above a staff with a treble clef:

Notice that each space and line above the staff gets a letter name with ledger lines, as if the staff were simply continuing upwards. The same is true for ledger lines below a staff, as shown in Example 10:

Notice that each space and line below the staff gets a letter name with ledger lines, as if the staff were simply continuing downwards.
- The Staff, Clefs, and Ledger Lines (musictheory.net)
- Flashcards for Treble, Bass, Alto, and Tenor Clefs (Richman Music School)
- Printable Treble Clef Flash Cards (Samuel Stokes Music) (pages 3 to 5)
- Printable Bass Clef Flash Cards (Samuel Stokes Music) (pages 1 to 3)
- Printable Alto Clef Flash Cards (Samuel Stokes Music)
- Printable Tenor Clef Flash Cards (Samuel Stokes Music)
- Paced Game: Treble Clef (Tone Savvy)
- Paced Game: Bass Clef (Tone Savvy)
- Paced Game: Alto Clef (Tone Savvy)
- Paced Game: Tenor Clef (Tone Savvy)
Easy
Medium
- Worksheets in Treble Clef (.pdf)
- Treble Clef with Ledger Lines (.pdf)
- Worksheets in Bass Clef (.pdf, .pdf)
- Bass Clef with Ledger Lines (.pdf)
- Worksheets in Alto Clef (.pdf, .pdf)
- Worksheets in Tenor Clef (.pdf)
Advanced
- All Clefs (.pdf)
Key Takeaways
- A beat is a pulse in music that regularly recurs.
- Simple meters are meters in which the beat divides into two, and then further subdivides into four.
- Duple meters have groupings of two beats, triple meters have groupings of three beats, and quadruple meters have groupings of four beats.
- There are different conducting patterns for duple, triple, and quadruple meters.
- A measure is equivalent to one group of beats (duple, triple, or quadruple). Measures are separated by bar lines.
- Time signatures in simple meters express two things: how many beats are contained in each measure (the top number), and the beat unit (the bottom number), which refers to the note value that is the beat.
- A beam visually connects notes together, grouping them by beat. Beaming changes in different time signatures.
- Notes below the middle line on a staff are up-stemmed, while notes above the middle line on a staff are down-stemmed. Flag direction works similarly.
In Rhythmic and Rest Values, we discussed the different rhythmic values of notes and rests. Musicians organize rhythmic values into various meters, which are—broadly speaking—formed as the result of recurrent patterns of accents in musical performances.
Terminology
Listen to the following performance by the contemporary musical group Postmodern Jukebox ( Example 1). They are performing a cover of the song "Wannabe" by the Spice Girls (originally released in 1996). Beginning at 0:11, it is easy to tap or clap along to this recording. What you are tapping along to is called a beat—a pulse in music that regularly recurs.
Example 1. A cover of "Wannabe" performed by Postmodern Jukebox; listen starting at 0:11.
Example 1 is in a simple meter: a meter in which the beat divides into two, and then further subdivides into four. You can feel this yourself by tapping your beat twice as fast; you might also think of this as dividing your beat into two smaller beats.
Different numbers of beats group into different meters. Duple meters contain beats that are grouped into twos, while Triple meters contain beats that are grouped into threes, and Quadruple meters contain beats that are grouped into fours.
Listening to Simple Meters
Let's listen to examples of simple duple, simple triple, and simple quadruple meters. A simple duple meter contains two beats, each of which divides into two (and further subdivides into four). "The Stars and Stripes Forever" (1896), written by John Philip Sousa, is in a simple duple meter.
Listen to Example 2, and tap along, feeling how the beats group into sets of two:
Example 2. "The Stars and Stripes Forever" played by the Dallas Winds.
A simple triple meter contains three beats, each of which divides into two (and further subdivides into four). Wolfgang Amadeus Mozart's "Minuet in F major," K.2 (1774) is in a simple triple meter. Listen to Example 3, and tap along, feeling how the beats group into sets of three:
Example 3. Mozart's "Minuet in F major," played by Alan Huckleberry.
Finally, a simple quadruple meter contains four beats, each of which divides into two (and further subdivides into four). The song "Cake" (2017) by Flo Rida is in a simple quadruple meter. Listen to Example 4 starting at 0:45 and tap along, feeling how the beats group into sets of four:
Example 4. "Cake" by Flo Rida; listen starting at 0:45.
As you can hear and feel (by tapping along), musical compositions in a wide variety of styles are governed by meter. You might practice identifying the meters of some of your favorite songs or musical compositions as simple duple, simple triple, or simple quadruple; listening carefully and tapping along is the best way to do this. Note that simple quadruple meters feel similar to simple duple meters, since four beats can be divided into two groups of two beats. It may not always be immediately apparent if a work is in a simple duple or simple quadruple meter by listening alone.
Conducting Patterns
If you have ever sung in a choir or played an instrument in a band or orchestra, then you have likely had experience with a conductor. Conductors have many jobs. One of these jobs is to provide conducting patterns for the musicians in their choir, band, or orchestra. Conducting patterns serve two main purposes: first, they establish a tempo, and second, they establish a meter.
The three most common conducting patterns outline duple, triple, and quadruple meters. Duple meters are conducted with a downward/outward motion (step 1), followed by an upward motion (step 2), as seen in Example 5. Triple meters are conducted with a downward motion (step 1), an outward motion (step 2), and an upward motion (step 3), as seen in Example 6. Quadruple meters are conducted with a downward motion (step 1), an inward motion (step 2), an outward motion (step 3), and an upward motion (step 4), as seen in Example 7:
Beat 1 of each of these measures is considered a downbeat . A downbeat is conducted with a downward motion, and you may hear and feel that it has more "weight" or "heaviness" then the other beats. An upbeat is the last beat of any measure. Upbeats are conducted with an upward motion, and you may feel and hear that they are anticipatory in nature.
Example 8 shows a short video demonstrating these three conducting patterns:
Example 8. Dr. John Lopez (Texas A&M University, Kingsville) demonstrates duple, triple, and quadruple conducting patterns.
You can practice these conducting patterns while listening to Example 2 (duple), Example 3 (triple), and Example 4 (quadruple) above.
Time Signatures
In Western musical notation, beat groupings (duple, triple, quadruple, etc.) are shown using bar lines, which separate music into measures (also called bars), as shown in Example 9. Each measure is equivalent to one beat grouping.

In simple meters, time signatures (also called meter signatures) express two things: 1) how many beats are contained in each measure, and 2) the beat unit (which note value gets the beat). Time signatures are expressed by two numbers, one above the other, placed after the clef (Example 10).

A time signature is not a fraction, though it may look like one; note that there is no line between the two numbers. In simple meters, the top number of a time signature represents the number of beats in each measure, while the bottom number represents the beat unit.
In simple meters, the top number is always 2, 3, or 4, corresponding to duple, triple, or quadruple beat patterns. The bottom number is usually one of the following:
- 2, which means the half note gets the beat.
- 4, which means the quarter note gets the beat.
- 8, which means the eighth note gets the beat.
You may also see the bottom number 16 (the sixteenth note gets the beat) or 1 (the whole note gets the beat) in simple meter time signatures.
There are two additional simple meter time signatures, which are 𝄴 (common time) and 𝄵 (cut time). Common time is the equivalent of [latex]\mathbf{^4_4}[/latex] (simple quadruple—four beats per measure), while cut time is the equivalent of [latex]\mathbf{^2_2}[/latex] (simple duple—two beats per measure).
Counting in Simple Meter
Counting rhythms aloud is important for musical performance; as a singer or instrumentalist, you must be able to perform rhythms that are written in Western musical notation. Conducting while counting rhythms is highly recommended and will help you to keep a steady tempo. Please note that your instructor may employ a different counting system. Open Music Theory privileges American traditional counting, but this is not the only method.
Example 11 shows a rhythm in a [latex]\mathbf{^4_4}[/latex] time signature, which is a simple quadruple meter. This time signature means that there are four beats per measure (the top 4) and that the quarter note gets the beat (the bottom 4).
- In each measure, each quarter note gets a count, expressed with Arabic numerals—"1, 2, 3, 4."
- When notes last longer than one beat (such as a half or whole note in this example), the count is held over multiple beats. Beats that are not counted out loud are written in parentheses.
- When the beat in a simple meter is divided into two, the divisions are counted aloud with the syllable “and,” which is usually notated with the plus sign (+). So, if the quarter note gets the beat, the second eighth note in each beat would be counted as “and.”
- Further subdivisions at the sixteenth-note level are counted as “e” (pronounced as a long vowel, as in the word “see”) and “a” (pronounced “uh”). At the thirty-second-note level, further subdivisions add the syllable “ta” in between each of the previous syllables.
Example 11. Rhythm in 4/4 time.
Simple duple meters have only two beats and simple triple meters have only three, but the subdivisions are counted the same way (Example 12).
Example 12. Simple duple meters have two beats per measure; simple triple meters have three.
Like with notes that last for two or more beats, beats that are not articulated because of rests, ties, and dots are also not counted out loud. These beats are usually written in parentheses, as shown in Example 13:
Example 13. Beats that are not counted out loud are put in parentheses.

When an example begins with a pickup note (anacrusis), your count will not begin on "1," as shown in Example 14. An anacrusis is counted as the last note(s) of an imaginary measure. When a work begins with an anacrusis, the last measure is usually shortened by the length of the anacrusis. This is demonstrated in Example 14: the anacrusis is one quarter note in length, so the last measure is only three beats long (i.e., it is missing one quarter note).
Counting with Beat Units of 2, 8, and 16
In simple meters with other beat units (shown in the bottom number of the time signature), the same counting patterns are used for the beats and subdivisions, but they correspond to different note values. Example 15 shows a rhythm with a [latex]\mathbf{^4_4}[/latex] time signature, followed by the same rhythms with different beat units. Each of these rhythms sounds the same and is counted the same. They are also all considered simple quadruple meters. The difference in each example is the bottom number of the time signature—which note gets the beat unit (quarter, half, eighth, or sixteenth).
Example 15. The same counted rhythm, as written in a meter with (a) a quarter-note beat, (b) a half-note beat, (c) an eighth-note beat, and (d) a sixteenth-note beat.
Beaming, Stems, Flags, and Multi-Measure Rests
Beams connect notes together by beat. As Example 16 shows, this means that beaming changes depending on the time signature. In the first measure, sixteenth notes are grouped into sets of four, because four sixteenth notes in a [latex]\mathbf{^4_4}[/latex] time signature are equivalent to one beat. In the second measure, however, sixteenth notes are grouped into sets of two, because one beat in a [latex]\mathbf{^4_8}[/latex] time signature is only equivalent to two sixteenth notes.
Example 16. Beaming in two different meters.

Note that in vocal music, beaming is sometimes only used to connect notes sung on the same syllable. If you are accustomed to music without beaming, you may need to pay special attention to beaming conventions until you have mastered them. In the top staff of Example 17, the eighth notes are not grouped with beams, making it difficult to see where beats 2 and 3 in the triple meter begin. The bottom staff shows that if we re-notate the rhythm so that the notes that fall within the same beat are grouped together with a beam, it makes the music much easier to read. Note that these two rhythms sound the same, even though they are beamed differently. The ability to group events according to a hierarchy is an important part of human perception, which is why beaming helps us visually parse notated musical rhythms—the metrical structure provides a hierarchy that we show using notational tools like beaming.
Example 18 shows several different note values beamed together to show the beat unit. The first line does not require beams because quarter notes are never beamed, but all subsequent lines do need beams to clarify beats.
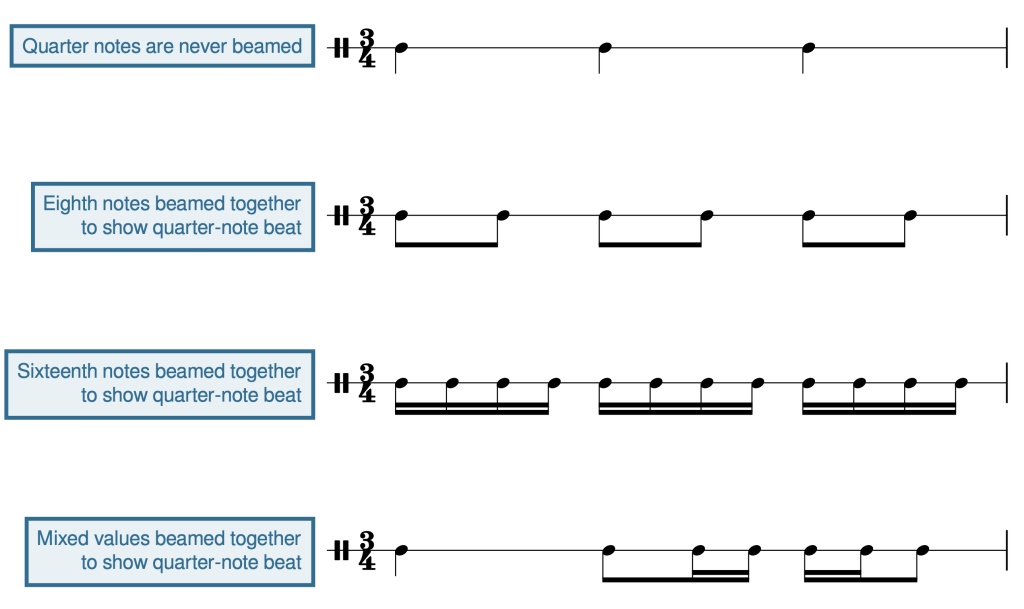

The second measure of Example 19 shows that when notes are grouped together with beams, the stem direction is determined by the note farthest from the middle line. On beat 1 of measure 2, this note is E5, which is above the middle line, so down-stems are used. Beat 2 uses up-stems because the note farthest from the middle line is the E4 below it.

Flagging is determined by stem direction (Example 20). Notes above the middle line receive a down-stem (on the left) and an inward-facing flag (facing right). Notes below the middle line receive an up-stem (on the right) and an outward-facing flag (facing left). Notes on the middle line can be flagged in either direction, usually depending on the contour of the musical line.
Partial beams can be used for mixed rhythmic groupings, as shown in Example 21. Sometimes these beaming conventions look strange to students who have had less experience with reading beamed music. If this is the case, you will want to pay special attention to how the notes in Example 21 are beamed.
Example 21. Partial beams are used for some mixed rhythmic groupings.
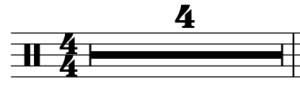
Rests that last for multiple full measures are sometimes notated as seen in Example 22. This example indicates that the musician is to rest for a duration of four full measures.
A Note on Ties
We have already encountered ties that can be used to extend a note over a measure line. But ties can also be used like beams to clarify the metrical structure within a measure. In the first measure of Example 23, beat 2 begins in the middle of the eighth note, making it difficult to see the metrical structure. Breaking the eighth note into two sixteenth notes connected by a tie, as shown in the second measure, clearly shows the beginning of beat 2.
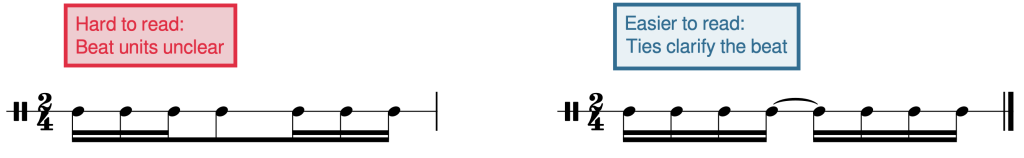
- Simple Meter Tutorial (musictheory.net)
- Video Tutorial on Simple Meter, Beats, and Beaming (YouTube)
- Conducting Patterns (YouTube)
- Simple Meter Time Signatures (liveabout.com)
- Video Tutorial on Counting Simple Meters (One Minute Music Lessons)
- Simple Meter Counting (YouTube)
- Beaming Rules (Music Notes Now)
- Beaming Examples (Dr. Sebastian Anthony Birch)
- Time Signatures and Rhythms (.pdf)
- Terminology, Bar Lines, Fill-in-rhythms, Re-beaming (.pdf)
- Meters, Time Signatures, Re-beaming (website)
- Bar Lines, Time Signatures, Counting (.pdf)
- Time Signatures, Re-beaming, p. 4 (.pdf)
- Fill-in-rhythms (.pdf)
- Time Signatures (.pdf, .pdf)
- Bar Lines (.pdf, .pdf, .pdf)
Notes whose exact pitch sounds somewhere between the flat and regular versions of a scale degree, particularly 3̂ and 7̂.

