VIII. 20th- and 21st-Century Techniques
102
Mark Gotham; Megan Lavengood; Brian Moseley; and Kris Shaffer
Key Takeaways
This chapter introduces a number of pitch collections that appealed to many composers in the 20th century:
- diatonic collection, as separate from major/minor scales or diatonic modes
- pentatonic collection: a five-note collection that corresponds to the black keys of the piano; can also be generated as a stack of five perfect fifths or through the pitch interval pattern 2–2–3–2–3
- whole-tone collection: a six-note collection that is made up entirely of notes separated by whole steps
- octatonic collection: an eight-note collection that is formed by alternating whole- and half steps
- hexatonic collection: a six-note collection generated with the pitch interval pattern 1–3–1–3–1–3
- acoustic collection: a seven-note collection similar to the mixolydian mode but with a [latex]\uparrow\hat{4}[/latex]; corresponds roughly to the lowest partials of the harmonic series
Other pitch collections introduced include:
- Olivier Messiaen's "modes of limited transposition": a group of scales that cannot be transposed in 12 unique ways
- The "distance model" of generating collections with a repeating pattern of pitch intervals
Beyond the use of major/minor and the diatonic modes, there are four new(ish) collections that occupy a special place in the 20th century: the pentatonic, whole-tone, octatonic, and acoustic collections. This chapter discusses these collections along with some important questions of modal properties and extra-musical meaning.
Diatonic Collection and Pandiatonicism
You have probably encountered the concept of the diatonic collection many times already, especially in the chapters on modes in pop and in 20th-/21st-century music, or even when you first learned about major and minor keys. The diatonic collection is the basis of much Western music.
In the 20th and 21st centuries, composers sometimes used the diatonic collection, but without making any attempt to make a specific pitch sound like the the pitch center. Such examples are not tonal, nor are they modal; instead, they are considered pandiatonic. Igor Stravinsky often wrote pandiatonic passages; many can be heard throughout the opening of his ballet Petrushka.
Pentatonic Collection
The pentatonic collection is prevalent in music across the globe. It is a collection built with the interval pattern ma2–ma2–mi3–ma2–mi3. The pentatonic collection can be described with reference to the diatonic modes in multiple different ways (Example 1).
- Using the scale degrees of a major scale, a pentatonic scale can be formed with [latex]\hat{1}\text{, }\hat{2}\text{, }\hat{3}\text{, }\hat{5}\text{, and }\hat{6}[/latex].
- If you think of the diatonic collection as a stack of perfect fifths (F, C, G, D, A, E, B), then the pentatonic is a narrower form of the same collection: C, G, D, A, E.
- Finally, if you visualize the piano, note that the complement of C, D, E, F, G, A, B, C (the white notes) is G♭, A♭, B♭, D♭, E♭ (the black notes). The black-note collection is, once again, the pentatonic.
https://musescore.com/user/32728834/scores/5990266/embed
Example 1. (a–c) Three ways of generating a pentatonic collection, and (d) a rotation of the pentatonic collection.
What the pentatonic collection removes from the diatonic is the two notes that create half steps ([latex]\hat{4}[/latex] and [latex]\hat{7}[/latex], if you are thinking in terms of major scale degrees). The absence of semitones arguably makes the pentatonic more readily rotatable and considered as a collection, without a strong emphasis on a particular note as tonic. Any member of the collection easily functions as a tonal center. For example, there are five unique modes of the collection given in (a) of Example 1, formed by rotating the collection so that each pitch class becomes tonic: C pentatonic (C, D, E, G, A), D pentatonic (D, E, G, A, C), E pentatonic (E, G, A, C, D), and so on. Letter (d) of Example 1 gives an especially common rotation of the pentatonic collection that is referred to as the minor pentatonic.
The pentatonic scale is especially common as a basis for melodic composition. One example can be heard during the first movement of Chen Yi's percussion concerto, at the entrance of the strings at 2:13. Notice that the pentatonic melody is sometimes accompanied by atonal-sounding chords in the brass. Pentatonic melodies don't need to be harmonized within the pentatonic collection, and in fact often aren't; after all, there are only two possible triads in the pentatonic collection (C major and A minor, for example, in the collection C–D–E–G–A).
Whole-Tone Collection
The whole-tone collection is exactly what it sounds like: a scale made up entirely of six whole steps. Similar to the pentatonic scale, the whole-tone scale is rotationally ambiguous, since there is only one size of step. Composers often exploit this ambiguity by using the whole-tone collection to produce an unsettled feeling in the listener (in film and TV, one famous trope is to use the whole-tone scale to accompany a dream sequence).
There are only two unique whole-tone collections: one that contains the even-numbered pitch classes [0, 2, 4, 6, 8, 10] and one that contains the odd-numbered pitch classes [1, 3, 5, 7, 9, 11]. If you need to distinguish between these two collections in an analysis, you can use the abbreviations WT0 and WT1: "WT" stands for "whole tone," and the subscript number indicates the pitch C (0) or C♯ (1) (Example 2).
https://musescore.com/user/32728834/scores/5990278/embed
Example 2. There are only two whole-tone collections. Transposing WT1 up a half step would yield WT0 again.
Octatonic Collection
The octatonic collection is built with an alternation of whole steps and half steps, leading to a total of eight distinct pitches (Example 3). Jazz musicians refer to this as the diminished scale, as it fits well with a fully diminished seventh chord. (Of course, there can be other scales that have eight distinct pitches, but this is the one called the octatonic scale.)
https://musescore.com/user/32728834/scores/5990299/embed
Example 3. There are only three octatonic collections.
The interval content of this collection is very homogeneous, and this intervallic consistency leads to one of its most interesting properties. As shown in Example 3, there are only three possible octatonic collections. When we transpose the first collection above (OCT0,1) by 3—adding 3 to each of the integers in the collection—<0, 1, 3, 4, 6, 7, 9, 10> becomes <3, 4, 6, 7, 9, 10, 0, 1>, which is the same as the first collection, just starting on a different pitch. If you need to distinguish between these two collections in an analysis, you can use the abbreviations OCT0,1, OCT1,2, and OCT2,3: "OCT" is an abbreviation of "octatonic," and the subscript numbers represent pitches that create a half step unique to that scale (C,C♯; C♯,D; and D,E♭, respectively).
Joan Tower frequently uses the octatonic collection, and it is particularly audible in the opening of her piece Silver Ladders.
Unlike the other collections discussed here, the octatonic collection appears with some frequency prior to the 20th century, especially in Russia.[1] The octatonic collection can produce several familiar triadic harmonies, as shown in Example 4: eight major/minor triads (and four diminished triads, not shown), and four each of every type of seventh chord except the major seventh chord. However, there are no chords related by root motion by fifth, so no tonic/dominant motion is possible. Instead, there is a plethora of root motion by third. Frédéric Chopin uses the octatonic over a B♭7 chord in his Ballade in G minor (Example 5). Thanks to all those triadic harmonies, it’s a versatile mode that can imply tonal associations while also inviting a freer movement among tonalities not traditionally regarded as being closely related.
https://musescore.com/user/32728834/scores/5992271/embed
Example 4. The octatonic collection contains many triadic harmonies.
https://musescore.com/user/32728834/scores/5992316/embed
Example 5. Octatonic collections in Chopin’s Ballade in G minor (1836).
Hexatonic Collection
The hexatonic collection is a six-note collection that is formed by alternating minor seconds and minor thirds. The name "hexatonic" refers to its six notes, and while there are other possible scales with six notes (for example, the blues scale), the name "hexatonic collection" always refers to this particular group of notes. Like octatonic collections, hexatonic collections can only be transposed four times before returning to the same group of notes again (Example 6), and they are similarly named according to their lowest semitone (e.g., HEX0,1 is the hexatonic collection containing C–C♯).
https://musescore.com/user/32728834/scores/6925856/embed
Example 6. Four possible hexatonic collections.
Again like octatonic collections, hexatonic collections contain triads but do not suggest a particular tonic chord or home key. As shown in Example 7, each collection contains three major triads, three minor triads, and two augmented triads. Juxtaposing two augmented triads that are one semitone apart is another way of generating the hexatonic scale.
https://musescore.com/user/32728834/scores/6925866/embed
Example 7. Triads present in a hexatonic collection.
Acoustic Collection
The acoustic collection is based on the lowest intervals of the overtone series. This is significant because there has long been an association between those lowest intervals and the notion of musical consonance. The result is a mode that resembles the major scale but with a [latex]\uparrow\hat{4}[/latex] and [latex]\downarrow\hat{7}[/latex] (Example 8).
https://musescore.com/user/32728834/scores/5992286/embed
Example 8. The acoustic scale is derived from the notes of the overtone series.
New Ways of Organizing Pitch
Many composers of the 20th and 21st centuries have looked for new ways of generating pitch collections for their music.
Messiaen's modes of limited transposition
Olivier Messiaen was interested in composing with collections that can only be transposed a few times before they repeat themselves, such as the octatonic collection. Messiaen’s “modes of limited transposition,” as he called them, are shown in the table in Example 9 and in notation in Example 10. The numbers in parentheses refer to pitch intervals in semitones.
[table “80” not found /]
Example 9. Messiaen's Modes of Limited Transposition.
https://musescore.com/user/32728834/scores/6925817/s/nEWWaR/embed
Example 10. Messiaen's modes of limited transposition, beginning on C.
These are not the only collections that have limited transpositions: other subsets/supersets of these collections may also have this property. Even within this set, Mode 1 is a subset of Modes 3 and 6. [2]
Distance model modes
Distance model modes involve a more restricted set of modes of limited transposition. These modes are formed with an alternation between two intervals, such as:
- 1:2 = alternating semi and whole tones (the octatonic mode again)
- 1:3 = semitones and minor thirds, sometimes called the hexatonic mode/collection, or in pitch-class set parlance, the "magic" hexachord
- 1:5 = semitones and perfect fourths
This style of organization is strongly associated with Béla Bartók, as we’ll see in the next chapter.
Other modes
This is just the tip of the iceberg, even for 20th-century classical music. Among the other main areas to explore are:
- Microtonal modes, beloved of Ligeti and the spectral school, which focus on alternate tuning systems and avoid any assumption of the equal-tempered 12.
- Synthetic modes, derived by alteration of diatonic, as in the non-standard key signatures of certain movements in Bartók's Mikrokosmos.
- One-off cases like the "scala enigmatica" of Verdi’s Ave Maria (which is hardly used as a scale/mode in any other case).
Important Considerations with Collections
Why do some of these modes keep cropping up in different contexts? Again, that’s a big issue that has attracted a great deal of theoretical attention. Here are some highlights:
- Correspondence to the natural overtone series. One hypothesis is that people like modes that see the important pitches align with those low down in the harmonic series, and thus with what are conventionally called consonances (octaves, fifths, etc.). Clearly the acoustic collection is a particularly literal implementation of this idea.
- Symmetry is a key preoccupation of 20th-century composers. One reason for this is the desire to create a new kind of order not rooted (pun intended…) in the "from-the-bass-up" world of the overtone series and fundamental bass harmony. Symmetry can be internal to scale, as in the rotational symmetry of the modes of limited transposition, or else between scales, as in Bartók's Cantata Profana.
- Maximal evenness. A prominent theory of modal construction emphasizes the even distribution of pitches in the space.[3] Think of the diatonic modes again. The diatonic collection is made up of mostly whole tones, with only two semitones that are as far away from each other as possible. This maximized spacing between the semitones means that the pitches of the diatonic collection are maximally even.
- Agmon, Eytan. 1990. “Equal Divisions of the Octave in a Scarlatti Sonata.” In Theory Only 11 (5): 1–8.
- Clough, John, and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35, no. 1–2 (Spring–Autumn): 93–173.
- Worksheet on collections (.pdf, .mscz). Asks students to spell one example of each of the collections from this chapter.
- Analyze Lili Boulanger's resplendent Hymne au Soleil. Identify modes and collections used, along with related techniques. Scores can be found on IMSLP and MuseScore. Both include the original French text and an English translation in the underlay.
1. A scale, mode, or collection that follows the pattern of whole and half steps W–W–H–W–W–W–H, or any rotation of that pattern.
2. Belonging to the local key (as opposed to "chromatic").
A pitch collection built with the interval pattern ma2–ma2–mi3–ma2–mi3. This collection can also be generated by using scale degrees 1̂, 2̂, 3̂, 5̂, and 6̂ only of the major scale.
A pitch collection composed entirely of whole steps. There are six whole steps in a whole tone collection, and there are only two possible whole tone scales: C–D–E–F♯–G♯–A♯, or C♯–D♯–F–G–A–B.
The octatonic collection is built with an alternation of whole steps and half steps, leading to a total of eight distinct pitches. One example is C–C♯–D♯–E–F♯–G–A–B♭. Jazz musicians refer to this as the diminished scale.
A six-note collection that alternates between half steps and minor thirds, such as C–C♯–E–F–G♯–A.
Pandiatonicism uses the notes of a diatonic collection without imparting a sense of pitch center.
A pentatonic scale with the intervals mi3–ma2–ma2–mi3–ma2. For example, starting on A, the minor pentatonic would be A–C–D–E–G. The minor pentatonic is a rotation of the major pentatonic.
A system of naming pitch classes that treats C as 0, C♯ as 1, D as 2, etc.
The distance between roots of adjacent chords. For example, "root motion by step" refers to the distance between two chords that are only one step apart, such as I and ii, IV and V, etc. Note that the root is not always in the bass, so this is a separate concept from bass motion.
A larger set that contains other smaller sets. For example, a superset of (037) is the diatonic collection, (013568t).
A group of pitch classes.
Key Takeaways
- A beat is a pulse in music that regularly recurs.
- Simple meters are meters in which the beat divides into two, and then further subdivides into four.
- Duple meters have groupings of two beats, triple meters have groupings of three beats, and quadruple meters have groupings of four beats.
- There are different conducting patterns for duple, triple, and quadruple meters.
- A measure is equivalent to one group of beats (duple, triple, or quadruple). Measures are separated by bar lines.
- Time signatures in simple meters express two things: how many beats are contained in each measure (the top number), and the beat unit (the bottom number), which refers to the note value that is the beat.
- A beam visually connects notes together, grouping them by beat. Beaming changes in different time signatures.
- Notes below the middle line on a staff are up-stemmed, while notes above the middle line on a staff are down-stemmed. Flag direction works similarly.
In Rhythmic and Rest Values, we discussed the different rhythmic values of notes and rests. Musicians organize rhythmic values into various meters, which are—broadly speaking—formed as the result of recurrent patterns of accents in musical performances.
Terminology
Listen to the following performance by the contemporary musical group Postmodern Jukebox ( Example 1). They are performing a cover of the song "Wannabe" by the Spice Girls (originally released in 1996). Beginning at 0:11, it is easy to tap or clap along to this recording. What you are tapping along to is called a beat—a pulse in music that regularly recurs.
Example 1. A cover of "Wannabe" performed by Postmodern Jukebox; listen starting at 0:11.
Example 1 is in a simple meter: a meter in which the beat divides into two, and then further subdivides into four. You can feel this yourself by tapping your beat twice as fast; you might also think of this as dividing your beat into two smaller beats.
Different numbers of beats group into different meters. Duple meters contain beats that are grouped into twos, while Triple meters contain beats that are grouped into threes, and Quadruple meters contain beats that are grouped into fours.
Listening to Simple Meters
Let's listen to examples of simple duple, simple triple, and simple quadruple meters. A simple duple meter contains two beats, each of which divides into two (and further subdivides into four). "The Stars and Stripes Forever" (1896), written by John Philip Sousa, is in a simple duple meter.
Listen to Example 2, and tap along, feeling how the beats group into sets of two:
Example 2. "The Stars and Stripes Forever" played by the Dallas Winds.
A simple triple meter contains three beats, each of which divides into two (and further subdivides into four). Wolfgang Amadeus Mozart's "Minuet in F major," K.2 (1774) is in a simple triple meter. Listen to Example 3, and tap along, feeling how the beats group into sets of three:
Example 3. Mozart's "Minuet in F major," played by Alan Huckleberry.
Finally, a simple quadruple meter contains four beats, each of which divides into two (and further subdivides into four). The song "Cake" (2017) by Flo Rida is in a simple quadruple meter. Listen to Example 4 starting at 0:45 and tap along, feeling how the beats group into sets of four:
Example 4. "Cake" by Flo Rida; listen starting at 0:45.
As you can hear and feel (by tapping along), musical compositions in a wide variety of styles are governed by meter. You might practice identifying the meters of some of your favorite songs or musical compositions as simple duple, simple triple, or simple quadruple; listening carefully and tapping along is the best way to do this. Note that simple quadruple meters feel similar to simple duple meters, since four beats can be divided into two groups of two beats. It may not always be immediately apparent if a work is in a simple duple or simple quadruple meter by listening alone.
Conducting Patterns
If you have ever sung in a choir or played an instrument in a band or orchestra, then you have likely had experience with a conductor. Conductors have many jobs. One of these jobs is to provide conducting patterns for the musicians in their choir, band, or orchestra. Conducting patterns serve two main purposes: first, they establish a tempo, and second, they establish a meter.
The three most common conducting patterns outline duple, triple, and quadruple meters. Duple meters are conducted with a downward/outward motion (step 1), followed by an upward motion (step 2), as seen in Example 5. Triple meters are conducted with a downward motion (step 1), an outward motion (step 2), and an upward motion (step 3), as seen in Example 6. Quadruple meters are conducted with a downward motion (step 1), an inward motion (step 2), an outward motion (step 3), and an upward motion (step 4), as seen in Example 7:
Beat 1 of each of these measures is considered a downbeat . A downbeat is conducted with a downward motion, and you may hear and feel that it has more "weight" or "heaviness" then the other beats. An upbeat is the last beat of any measure. Upbeats are conducted with an upward motion, and you may feel and hear that they are anticipatory in nature.
Example 8 shows a short video demonstrating these three conducting patterns:
Example 8. Dr. John Lopez (Texas A&M University, Kingsville) demonstrates duple, triple, and quadruple conducting patterns.
You can practice these conducting patterns while listening to Example 2 (duple), Example 3 (triple), and Example 4 (quadruple) above.
Time Signatures
In Western musical notation, beat groupings (duple, triple, quadruple, etc.) are shown using bar lines, which separate music into measures (also called bars), as shown in Example 9. Each measure is equivalent to one beat grouping.

In simple meters, time signatures (also called meter signatures) express two things: 1) how many beats are contained in each measure, and 2) the beat unit (which note value gets the beat). Time signatures are expressed by two numbers, one above the other, placed after the clef (Example 10).

A time signature is not a fraction, though it may look like one; note that there is no line between the two numbers. In simple meters, the top number of a time signature represents the number of beats in each measure, while the bottom number represents the beat unit.
In simple meters, the top number is always 2, 3, or 4, corresponding to duple, triple, or quadruple beat patterns. The bottom number is usually one of the following:
- 2, which means the half note gets the beat.
- 4, which means the quarter note gets the beat.
- 8, which means the eighth note gets the beat.
You may also see the bottom number 16 (the sixteenth note gets the beat) or 1 (the whole note gets the beat) in simple meter time signatures.
There are two additional simple meter time signatures, which are 𝄴 (common time) and 𝄵 (cut time). Common time is the equivalent of [latex]\mathbf{^4_4}[/latex] (simple quadruple—four beats per measure), while cut time is the equivalent of [latex]\mathbf{^2_2}[/latex] (simple duple—two beats per measure).
Counting in Simple Meter
Counting rhythms aloud is important for musical performance; as a singer or instrumentalist, you must be able to perform rhythms that are written in Western musical notation. Conducting while counting rhythms is highly recommended and will help you to keep a steady tempo. Please note that your instructor may employ a different counting system. Open Music Theory privileges American traditional counting, but this is not the only method.
Example 11 shows a rhythm in a [latex]\mathbf{^4_4}[/latex] time signature, which is a simple quadruple meter. This time signature means that there are four beats per measure (the top 4) and that the quarter note gets the beat (the bottom 4).
- In each measure, each quarter note gets a count, expressed with Arabic numerals—"1, 2, 3, 4."
- When notes last longer than one beat (such as a half or whole note in this example), the count is held over multiple beats. Beats that are not counted out loud are written in parentheses.
- When the beat in a simple meter is divided into two, the divisions are counted aloud with the syllable “and,” which is usually notated with the plus sign (+). So, if the quarter note gets the beat, the second eighth note in each beat would be counted as “and.”
- Further subdivisions at the sixteenth-note level are counted as “e” (pronounced as a long vowel, as in the word “see”) and “a” (pronounced “uh”). At the thirty-second-note level, further subdivisions add the syllable “ta” in between each of the previous syllables.
Example 11. Rhythm in 4/4 time.
Simple duple meters have only two beats and simple triple meters have only three, but the subdivisions are counted the same way (Example 12).
Example 12. Simple duple meters have two beats per measure; simple triple meters have three.
Like with notes that last for two or more beats, beats that are not articulated because of rests, ties, and dots are also not counted out loud. These beats are usually written in parentheses, as shown in Example 13:
Example 13. Beats that are not counted out loud are put in parentheses.

When an example begins with a pickup note (anacrusis), your count will not begin on "1," as shown in Example 14. An anacrusis is counted as the last note(s) of an imaginary measure. When a work begins with an anacrusis, the last measure is usually shortened by the length of the anacrusis. This is demonstrated in Example 14: the anacrusis is one quarter note in length, so the last measure is only three beats long (i.e., it is missing one quarter note).
Counting with Beat Units of 2, 8, and 16
In simple meters with other beat units (shown in the bottom number of the time signature), the same counting patterns are used for the beats and subdivisions, but they correspond to different note values. Example 15 shows a rhythm with a [latex]\mathbf{^4_4}[/latex] time signature, followed by the same rhythms with different beat units. Each of these rhythms sounds the same and is counted the same. They are also all considered simple quadruple meters. The difference in each example is the bottom number of the time signature—which note gets the beat unit (quarter, half, eighth, or sixteenth).
Example 15. The same counted rhythm, as written in a meter with (a) a quarter-note beat, (b) a half-note beat, (c) an eighth-note beat, and (d) a sixteenth-note beat.
Beaming, Stems, Flags, and Multi-Measure Rests
Beams connect notes together by beat. As Example 16 shows, this means that beaming changes depending on the time signature. In the first measure, sixteenth notes are grouped into sets of four, because four sixteenth notes in a [latex]\mathbf{^4_4}[/latex] time signature are equivalent to one beat. In the second measure, however, sixteenth notes are grouped into sets of two, because one beat in a [latex]\mathbf{^4_8}[/latex] time signature is only equivalent to two sixteenth notes.
Example 16. Beaming in two different meters.

Note that in vocal music, beaming is sometimes only used to connect notes sung on the same syllable. If you are accustomed to music without beaming, you may need to pay special attention to beaming conventions until you have mastered them. In the top staff of Example 17, the eighth notes are not grouped with beams, making it difficult to see where beats 2 and 3 in the triple meter begin. The bottom staff shows that if we re-notate the rhythm so that the notes that fall within the same beat are grouped together with a beam, it makes the music much easier to read. Note that these two rhythms sound the same, even though they are beamed differently. The ability to group events according to a hierarchy is an important part of human perception, which is why beaming helps us visually parse notated musical rhythms—the metrical structure provides a hierarchy that we show using notational tools like beaming.
Example 18 shows several different note values beamed together to show the beat unit. The first line does not require beams because quarter notes are never beamed, but all subsequent lines do need beams to clarify beats.
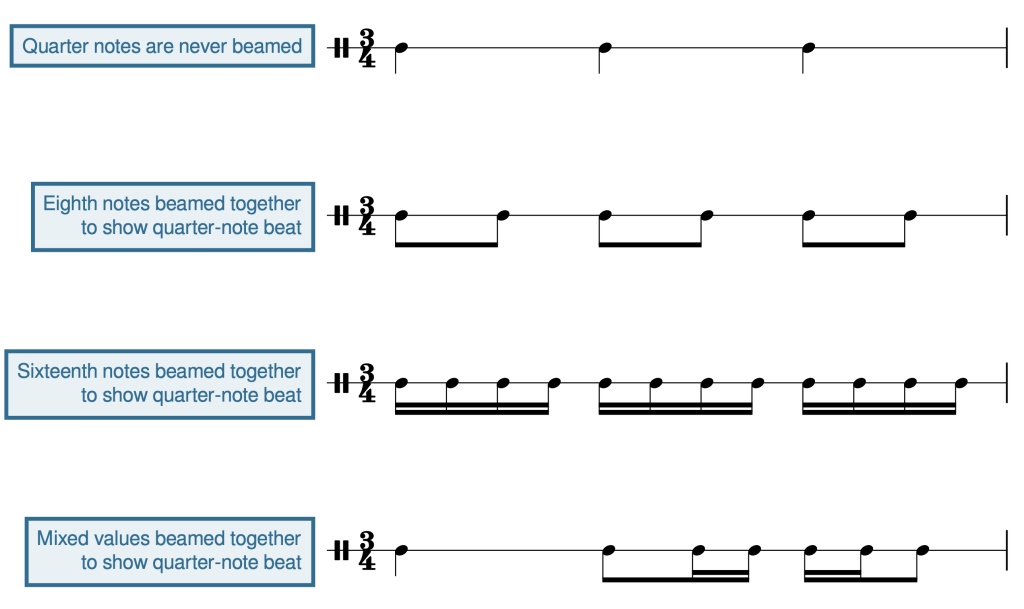

The second measure of Example 19 shows that when notes are grouped together with beams, the stem direction is determined by the note farthest from the middle line. On beat 1 of measure 2, this note is E5, which is above the middle line, so down-stems are used. Beat 2 uses up-stems because the note farthest from the middle line is the E4 below it.

Flagging is determined by stem direction (Example 20). Notes above the middle line receive a down-stem (on the left) and an inward-facing flag (facing right). Notes below the middle line receive an up-stem (on the right) and an outward-facing flag (facing left). Notes on the middle line can be flagged in either direction, usually depending on the contour of the musical line.
Partial beams can be used for mixed rhythmic groupings, as shown in Example 21. Sometimes these beaming conventions look strange to students who have had less experience with reading beamed music. If this is the case, you will want to pay special attention to how the notes in Example 21 are beamed.
Example 21. Partial beams are used for some mixed rhythmic groupings.
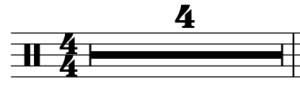
Rests that last for multiple full measures are sometimes notated as seen in Example 22. This example indicates that the musician is to rest for a duration of four full measures.
A Note on Ties
We have already encountered ties that can be used to extend a note over a measure line. But ties can also be used like beams to clarify the metrical structure within a measure. In the first measure of Example 23, beat 2 begins in the middle of the eighth note, making it difficult to see the metrical structure. Breaking the eighth note into two sixteenth notes connected by a tie, as shown in the second measure, clearly shows the beginning of beat 2.
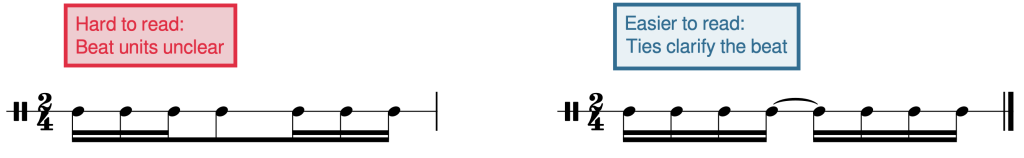
- Simple Meter Tutorial (musictheory.net)
- Video Tutorial on Simple Meter, Beats, and Beaming (YouTube)
- Conducting Patterns (YouTube)
- Simple Meter Time Signatures (liveabout.com)
- Video Tutorial on Counting Simple Meters (One Minute Music Lessons)
- Simple Meter Counting (YouTube)
- Beaming Rules (Music Notes Now)
- Beaming Examples (Dr. Sebastian Anthony Birch)
- Time Signatures and Rhythms (.pdf)
- Terminology, Bar Lines, Fill-in-rhythms, Re-beaming (.pdf)
- Meters, Time Signatures, Re-beaming (website)
- Bar Lines, Time Signatures, Counting (.pdf)
- Time Signatures, Re-beaming, p. 4 (.pdf)
- Fill-in-rhythms (.pdf)
- Time Signatures (.pdf, .pdf)
- Bar Lines (.pdf, .pdf, .pdf)

