I. Fundamentals
20 Roman Numerals and SATB Chord Construction
Samuel Brady and Kris Shaffer
Key Takeaways
- Roman numeral analysis is an analytical procedure in which musicians use Roman numerals to identify chords within the context of key signatures.
- Roman numerals identify the scale degree of the chord's root, the chord's quality, and any extensions or inversions the chord may include.
- Uppercase Roman numerals denote major triads, and lowercase Roman numerals denote minor triads. A o symbol after a lowercase Roman numeral represents a diminished triad, while a + sign after an uppercase Roman numeral represents an augmented triad.
- The Roman numeral quality of a seventh chord is dependent on the chord's triad; the exceptions are half-diminished and fully diminished seventh chords, whose qualities are dependent on their chordal seventh.
- When constructing a chord in SATB style, there are six rules to keep in mind: stem direction, chord construction, range, spacing, voice crossing, and doubling.
Writing Roman Numerals
Music theorists use Roman numerals to identify chords within the context of key signatures. Roman numerals identify the scale degree of the chord's root, the chord's quality, and any extensions or inversions the chord may include. Because Roman numerals convey the same information across major and minor key signatures, using them can save time in analyzing Western common practice music.
The three columns of Example 1 show the Arabic numerals 1 through 7 alongside the corresponding uppercase and lowercase Roman numerals.
[table “68” not found /]
Example 1. Arabic and Roman numerals.
To type uppercase Roman numerals, use the uppercase Latin alphabet letters “I” and “V”; likewise, for lowercase Roman numerals, type the lowercase “i” and “v.” The Roman numerals IV (4) and VI (6) are often confused; to remember the difference, think of IV (4) as V minus I (5 minus 1), and VI (6) as V plus I (5 plus 1).

Handwritten uppercase Roman numerals have horizontal bars across the top and bottom of the numeral, in order to further distinguish between uppercase and lowercase (Example 2). There is no such difference with lowercase Roman numerals.
Roman Numerals and Triad Quality
Roman numerals indicate three things: the scale degree of a chord's root, the quality of the chord, and the chord's inversion (see Inversion below). The number represented by the Roman numeral (see Example 1) corresponds to the scale degree of the chord’s root in whatever key the music is in. Uppercase Roman numerals denote major triads, and lowercase Roman numerals denote minor triads. For example, in a major key, a chord built on the first scale degree, [latex]\hat1[/latex] or do, is identified as “I,” and a chord built on the second scale degree, [latex]\hat2[/latex] or re, is identified by the lowercase Roman numeral “ii.” Lowercase Roman numerals followed by a superscript "o" (such as viio) represent diminished triads. Uppercase Roman numerals followed by a + sign (for example, the rare V+) represent augmented triads.
In the analysis of Western music, Roman numerals are generally placed below the bottom staff. Some music theorists prefer to use only uppercase Roman numerals, a system which assumes chord quality is intuited; in this textbook, we privilege the distinction of triadic qualities as denoted by uppercase and lowercase Roman numerals.
Example 3 shows the triads and seventh chords of a G major scale, labeled with chord symbols and now Roman numerals (in blue). The solfège and scale degree of the roots are also labeled.
https://musescore.com/user/32728834/scores/8514239/embed
Example 3. Roman numerals of triads in major and minor keys.
The Roman numerals and qualities of triads in major keys are as follows:
- I: major
- ii: minor
- ⅲ: minor
- IV: major
- V: major
- vi: minor
- vii°: diminished
The Roman numerals and qualities of triads in minor keys are as follows:
-
- ⅰ: minor
- ii°: diminished
- III: major
- iv: minor
- v: minor
- V: major (raised leading tone)
- VI: major
- VII: major
- vii°: diminished (raised leading tone)
Note that the quality of v/V and VII/viio differs depending on whether or not the leading tone is raised.
Roman Numerals and Seventh Chord Quality
Roman numeral labels for seventh chords add a superscript 7: for example, V7, ii7, and viio7. The capitalization of the Roman numeral depends on the quality of its triad: uppercase for a major triad (e.g., V7), lowercase for a minor or diminished triad (e.g., ii7). Half-diminished and fully diminished seventh chords, which both contain a diminished triad, are distinguished by an additional symbol after the lowercase Roman numeral: ∅ for half-diminished (e.g., vii∅7) and o for fully diminished (e.g., viio7).
Example 4 shows the triads and seventh chords of a G minor scale labeled with chord symbols and now Roman numerals (in blue). The solfège and scale degree of the roots are also labeled.
https://musescore.com/user/32728834/scores/8514287/embed
Example 4. Roman numerals of seventh chords in major and minor keys.
The Roman numeral and qualities of seventh chords in major keys are as follows:
-
- I7: major-major seventh (major seventh)
- ii7: minor-minor seventh (minor seventh)
- ⅲ7: minor-minor seventh (minor seventh)
- IV7: major-major seventh (major seventh)
- V7: major-minor seventh (dominant seventh)
- vi7: minor-minor seventh (minor seventh)
- vii∅7: half-diminished seventh
The Roman numeral and qualities of seventh chords in minor keys are as follows:
-
- ⅰ7: minor-minor seventh (minor seventh)
- ii∅7: half-diminished seventh
- III7: major-major seventh (major seventh)
- iv7: minor-minor seventh (minor seventh)
- v7: minor-minor seventh (minor seventh)
- V7: major-minor seventh (dominant seventh)
- VI7: major-major seventh (major seventh)
- VII7: major-minor seventh (dominant seventh)
- vii°7: fully diminished seventh (diminished seventh)
Note that the quality of v7/V7 and VII7/viio7 differs depending on whether or not the leading tone is raised.
Additionally, major seventh and dominant seventh chords have the same Roman numeral nomenclature; in other words, a I7 chord and a V7 chord are written the same even though the former is a major seventh chord and the latter is a dominant seventh chord. The difference would be discerned from the musical context.
Inversion
Roman numerals also denote inversions, shown through figured bass symbols placed after the Roman numeral (see the Inversion and Figured Bass chapter). For example, a superscript 6 represents a first inversion triad, and the figures [latex]^4_3[/latex] would indicate a second inversion seventh chord. Example 5 shows four different inverted chords with Roman numerals:
https://musescore.com/user/32728834/scores/6869635/embed
Example 5. Four inverted chords with Roman numerals and figures.
Roman Numeral Analysis
To complete a Roman numeral analysis, begin by identifying the work’s key and writing it under the key signature at the beginning of the work, using an uppercase letter name for a major key and a lowercase letter name for a minor key. It can also be helpful to write a lowercase “m” following the letter name of a minor key (e.g., “dm” for D minor). Be sure to apply any applicable accidental (e.g., “E♭” for E-flat major).
After you identify and write the key at the start of the work, follow these steps for each chord to complete the Roman numeral analysis:
-
- If a chord is in inversion, stack it in root position (preferably mentally).
- Identify all the notes of the chord, taking its quality into account.
- Write the Roman numeral that corresponds with the scale degree of the chord's root, reflecting the quality in the Roman numeral (uppercase or lowercase).
- Write any additional quality symbols ( o, ∅, +) as needed.
- Write figures after the Roman numeral.
Example 6 shows a Roman numeral analysis for Johann Sebastian Bach's chorale "Jesu meiner Seelen Wonne" (1642), which translates to "Jesus, delight of my soul." When analyzing this chorale, ignore the notes in parentheses. It is recommended that you cover up the Roman numerals in this example and try to generate them on your own before uncovering them:
https://musescore.com/user/32728834/scores/6867245/embed
Example 6. Roman numeral analysis of an excerpt of Johann Sebastian Bach's "Jesu, meiner Seelen Wonne" (BWV 359).
Roman numeral analysis is not just limited to chorales; indeed, you can apply them to many different genres of music. Example 7 shows an excerpt from "Caro Mio Ben" (c. 1783), which translates to "Dearly beloved" and is attributed to Guiseppe Giodani, with a Roman numeral analysis:
https://musescore.com/user/32728834/scores/6867246/embed
Example 7. Roman numeral analysis of an excerpt of Giuseppe Giordani's "Caro Mio Ben."
When the same chord occurs two or more times in a row, which is common, you can choose whether to repeat the Roman numeral (as in measure 1 of Example 7) or not (as in measure 2 of Example 6).
Writing Chords in SATB Style
Music theorists sometimes simplify compositions into four parts (or voices) in order to make their harmonic content more readily accessible. This practice is called SATB style, abbreviated after the four common voice parts of a choir––soprano (S), alto (A), tenor (T), and bass (B). When constructing a chord in strict SATB style, there are six rules musicians generally follow:
These six parameters form the basis of counterpoint and part writing, explored further in the sections Counterpoint and Galant Schemas and Diatonic Harmony, Tonicization, and Modulation.
Stem Direction

On a grand staff in SATB style, the soprano and alto are written in the treble clef (upper staff), while the tenor and bass are written in the bass clef (lower staff). The soprano and tenor voices receive up-stems, while the alto and bass parts receive down-stems. If the stem direction is crossed, this is an error. Example 8 shows a chord with incorrect stemming, followed by the corrected version.
Chord Construction

Be sure to check each chord for correct notes and accidentals, and make sure that your chords are not missing any notes. In Example 9, the first chord has accidentals erroneously added to two of the pitches, which are removed in the second chord to create a correct B diminished triad in first inversion.
The bass voice must always correspond with the inversion that the Roman numeral's figures indicate. However, the order of the upper notes can be arranged in many ways. In other words, there is not necessarily just one correct way to voice a chord.
Range
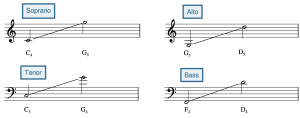
There is a generally accepted range for each voice (Example 10):
- Soprano - C4 to G5
- Alto - G3 to D5
- Tenor - C3 to G4
- Bass - F2 to D4

In Example 11, the soprano and bass notes are out of range; this is corrected by moving the soprano note down by an octave and the bass note up by an octave.
Spacing

There should be no more than an octave between adjacent upper voices (soprano and alto, alto and tenor) and no more than a twelfth between the tenor and bass. The most common spacing error occurs between the alto and tenor because the notes appear in different clefs. Example 12 first shows a chord with incorrect spacing—the soprano and alto are more than an octave apart, as are the alto and tenor—followed by a corrected version:
Voice Crossing

The ranges of voices should not cross. In other words, the soprano must always be higher than the alto, the alto must always be higher than the tenor, and the tenor must always be higher than the bass. In Example 13, the alto and tenor voices are crossed. This error is also the most common between the alto and tenor voices.
Doubling
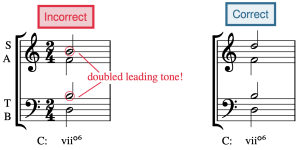
In a triad, the note in the bass is usually doubled in an upper voice. However, there is an exception to this: the leading tone is never doubled. Other tendency tones, such as chordal sevenths, are also never doubled. Seventh chords don't have any notes doubled because they contain four notes, one for each voice part. Incorrect doubling is seen in the first measure of Example 14, where the leading tone is doubled, followed by a corrected voicing in the second measure.
- Roman Numeral Analysis: Triads (musictheory.net)
- Harmonizing Scales & Roman Numeral Analysis (Kaitlan Bove)
- Roman Numerals (learnmusictheory.net)
- Roman Numeral Analysis (Phillip Magnuson)
- Roman Numeral Analysis (8notes.com)
- Roman Numeral Chord Symbols (Robert Hutchinson)
- Roman Numerals in Major Flashcards (gmajormusictheory.org)
- Roman Numerals in Minor Flashcards (gmajormusictheory.org)
- Inversion & Roman Numerals in Major Flashcards (gmajormusictheory.org)
- Inversion & Roman Numerals in Minor Flashcards (gmajormusictheory.org)
- How the Roman Numeral System Works (YouTube)
- Roman Numeral Identification, pp. 15–16, 18 (.pdf), pp. 5–7 (.pdf), pp. 1, 3, 4 (.pdf), (.pdf, .pdf, .pdf, .pdf)
- Roman Numeral Identification and Construction, p. 14 (triads) and 17 (seventh chords) (.pdf), p. 11 (.pdf), p. 8 (.pdf), p. 5 (.pdf), (website, website)
- Roman Numeral Construction, p. 22 (.pdf)
A single step within a scale; usually indicated by either a solfège syllable or an Arabic numeral with a caret.
A term that summarizes the quality of the third, fifth, and seventh (if applicable) above the root of the chord. Common chord qualities are major, minor, diminished, half-diminished, dominant, and augmented.
Key Takeaways
- where it came from: not only Schoenberg, but also Hauer and others
- what it’s "really" about: a new world order, and if so an equalising or totalising one?
- tonal precedents in Bach and Haydn, and "tonal tone rows" in (for example) Alban Berg, Hale Smith, and Benjamin Britten
- "total" or "integral" serialism in (for example) Ruth Crawford Seeger, Milton Babbitt, Olivier Messiaen, Karlheinz Stockhausen, Pierre Boulez.
Why Serialism? What’s the Attraction?
Some grand narratives of 20th-century music cast atonality as a logical consequence of a historical trend toward ever more chromaticism, and serialism as a matter of creating a radically different kind of structure out of the total chromatic. It would appear to achieve that end, at least for composers who joined Schoenberg in viewing it as a “method of composing with twelve tones which are related only with one another” (1950, 107)—contrast that with the fundamentally hierarchical tonal system. It may not be coincidental that it emerged in interwar Europe, when there may well have been a desire to start anew.
Equal tones? A new world order? Maybe, but the method has served a wide range of composers with correspondingly diverse aims, so it’s not so straightforward to summarize. There’s also a totalizing angle here that’s rather less utopian. Schoenberg is famously alleged to have described "his" discovery as one "which will ensure the supremacy of German music for the next hundred years" (qtd. in Stuckenschmidt 1977, 277). Schoenberg may or may not have actually said this, but Boulez definitely did later describe every composer to have remained "outside the serial experiments" since their discovery as "useless" ("Schönberg est mort," Score, 1952, reproduced in Notes of an Apprenticeship, 1968, 274).
A Series of Precedents?
There is a great deal of precedent for general forms of musical thinking pertinent to serial technique, from simple melodic inversion to furiously complex crab canons, and certain works like Bach’s Art of Fugue are notable partly for the strictness and comprehensiveness of design in general, and the healthy dose of "mirror writing" in particular.
In these cases, the mirror is usually "horizontal," giving versions of the twelve-tone technique’s I-form. The R-form of retrograde symmetry (given by a "vertical" mirror, if you will) is a primarily 20th-century concern, serial and otherwise. Non-serial 20th-century examples include a great deal of Bartók, the prelude/postlude pair in Hindemith's Ludus Tonalis, and Britten's Cantata Academica mvt. 2 (tellingly titled Alla rovescio). There are earlier examples, such as the Menuet al Roverso from Haydn’s Symphony no. 47 in G, but they are very rare.
There are (equally rare and also rather dubious) cases of tonal works that are said to exhibit the specifically twelve-tone practice of rotating through all the pitches. Often-cited examples include the choice of keys in the development of the finale to Mozart’s Symphony no. 40.
Conversely, there are 20th-century composers who wrote music that is serially organized in the sense that we would recognize, but in such a way as to embrace the sound world of an extended tonality (Example 1). Examples of this include:
- Alban Berg's Violin Concerto, with its row centered on triads and fifths.
- Hale Smith's Evocation, which the composer notes to have an "affinity" with jazz. Among the "jazzy" and/or "tonal" elements of this piece is the foregrounding of set [0,2,7], which the scholar Horace J. Maxile Jr. links to "the quartal harmonic and improvisational stylings of bop and post-bop schools" (2004, 125).
- Benjamin Britten’s Turn of the Screw, which adopts a similarly quartal structure in the row from which both the theme and tonal centers for the acts are serially organized.
Example 1. Tonal Tone Rows by FourScoreAndMore
Speaking of "tonal serialism," the trappings of tonality are not limited to pitch: what composers do with the other parameters is equally important. It's often observed (usually critically) that Schoenberg's early serial works may have used the twelve-tone technique in the pitch domain, but still adopted tonal forms, rhythms, and idioms such as waltzes.
The Emergence and Evolution of the Twelve-Tone Technique
Schoenberg is intimately associated with the twelve-tone technique and was quite content to describe it as "his" discovery (as above), though many people arrived at the idea largely independently around the same time, notably including Josef Matthias Hauer and Herbert Eimert. Schoenberg famously discussed relevant considerations like the "emancipation of the dissonance" early on, but his thoughts on serialism only emerged later, after those two others.
Hauer’s theory as expressed in his Zwölftontechnik: Die Lehre von den Tropen (1926) is notable for its early formalization of the twelve-tone technique and for organizing the millions of possibilities into 44 "tropes" (types) of tone rows in four groups based on symmetries among the unordered hexachords (with the prefixes Poly-, Mono-, Endo-, and Exo-).
After the first generation of "classic" serialists, we start to see a wider range of serial practices emerge, including a move toward "integral" or "total" serialism, which applies serial technique to parameters other than pitch, particularly rhythm, dynamics, and articulation. I say "after," but Ruth Crawford Seeger was already writing what later came to be known as integral or total serialism as early as c. 1930.
The most frequently cited examples came later, in a burst around 1950:
- Milton Babbitt: Three Compositions for Piano (1947)
- Olivier Messiaen: Mode de valeurs et dʼintensités for piano (1949–50)
- Karlheinz Stockhausen: Kreuzspiel for oboe, bass clarinet, piano, and two percussion (1951)
- Pierre Boulez: Structures 1 for two pianos (1952)
There were also signs of this mentality already in those "classic" early works. For instance, in the first movement of Webern’s Symphonie Op.21 (discussed further in this chapter), the exposition sees pitch classes fixed in specific registers, and his Op. 27 Variations for Piano has pitches, durations, and dynamics all aligned (for instance, B and G♯ are always eight notes, legato, and forte).
The span of notes a voice or instrument can produce.
Duplicating some notes of a chord in multiple parts.
Ordering the notes of a chord so that it is entirely stacked in thirds. The root of the chord is on the bottom.
The act of mirroring pitch content vertically, so that motion down becomes up and up becomes down. Inversion often preserves intervallic content.
Key Takeaways
- a timbral cadence
- a smooth structural boundary;
- an "attack-sustain" ("resonance") effect
- a seamless orchestral crescendo
- a timbrally nuanced melody
For a timbral cadence
Apart from changing the timbral distribution between sections (after a cadence), some composers make changes for the cadence itself, emphasizing the cadential moment. This is related to the more formal considerations of holding back a timbre discussed in the previous chapter.
Classical-era orchestral composers sometimes used wind parts in this way. Here’s an example from the opening of Mozart’s Piano Concerto K453, movement 3. The strings begin, and the timbral cadences are marked by the addition of winds (highlighted in the example).
Shostakovich provides some extraordinary 20th-century examples of this device. Consider the end of Shostakovich 11/iii. The outer sections of this movement are effectively one long viola solo, and the timbral addition of unison violins at the end is integral to formalizing the end of the theme. The melodic contour and discontinuation of the countersubject are also contributing, but the harmony is deeply ambiguous. In the following recording, the theme plays from 0’50” and the timbral cadences fall at the ends of the sections (4’50” and 12’40”).
https://open.spotify.com/track/75N4wFxecJ1tPdy4Jvc2d1?si=_5kv3h_YTT2egr3f3OHcxQ
This device is not unique to orchestral music. For instance, Blink 182 uses the same effect to close verses in the song "I Miss You": here the timbral cadence is achieved by the addition of the other vocalist (e.g., at 0'55").
To finesse a structural boundary
Timbral additions can also be used in the opposite sense: to finesse a structural boundary and actively connect the two sections. This is a favored device of Brahms. Brahms 2/iii opens with a gracious oboe theme, and it is the return of the oboe (in tandem with motivic handling and other matters) that finesses the return to the A section at m. 101/107.
It is the oboe again that Brahms adds to round out the first cadence of Brahms 4/i. (Note also the cello-viola dovetailing here.)
For the "attack-sustain" ("resonance") effect
One technique beloved of 20th-century composers is the "attack-sustain" or "resonance" effect. Acoustics teaches us that the very start of a note has a very different profile from the rest, and composers seem to be striving for something similar in orchestral writing that casts some instruments in an "attacking" role (shorter notes at the start) and others as "sustain" (longer notes starting together on the same pitches).
Examples abound and are not limited to the 20th century. For instance:
- Mozart: Magic Flute overture. When the brass parts enter, the horns are long, while the trumpets and trombones are short.
- Mozart: Dies Irae (from the Requiem): again, trumpets and drums are short; others long.
- Beethoven: The opening of Symphony 1/i is an iconic example, and not only for the extraordinary harmonies. The winds’ fp chords achieve the attack-sustain pair on their own, and are enhanced by string pizzicato (attack only).
In the 20th century, Schoenberg’s groundbreaking "Farben" (no. 3 from Five Orchestral Pieces) includes this effect (e.g., see the harp at reh. 2), and Britten uses it to magnificent effect in movement iii of the Four Sea Interludes. Play the following example from c. 0’45”.
https://open.spotify.com/track/6DEBxm5XrqUfvkqH1Pc3OR?si=Gy9UQTwUShaFIqwXRVq0EQ
Britten uses penetrating instruments for the attacks (including the harp again) and sets the resonance on sustained flute lines, as shown in this small excerpt:

(Note the octave transposition of the harp harmonics.) Later in the movement (around reh. 3), the same device appears with xylophone and piccolo on attack, and trumpet sustaining.
This practice is related to the wider device of employing different articulations on doublings of the same melodic line. Clear examples include:
- Debussy: La Mer / iii (fig. 55). The oboe has repeated notes; the flute does not.
- Sibelius: En Saga: m. 189, (viola pizz. + arco); m. 290 (trumpet staccato with oboe legato), then oboe with viola.
This, in turn, is related to the practice of having string parts play melodies tremolo for loud sections as seen in the Grieg example from the previous chapter.
For a seamless orchestral crescendo
That Grieg example displayed the kind of step-by-step orchestral crescendo that some composers turned into an extremely subtle process. Consider the following example of two extracts from Wagner’s Parsifal. The melody is in unison, and in both cases, a timbre is added at the top of the crescendo. In both cases, a higher, brighter version of an instrument already in the mix is added. In the second case, this is partly for registral reasons (the oboe replaces the bassoon in a high register); in both cases it transforms the sound, very subtly adding a timbral dimension to mark the moment in question.
Once again, it falls to the 20th century to furnish us with the truly iconic example of this process. Listen to this short crescendo from niente from Berg’s Wozzeck (preferably on good speakers, and having warned the neighbors!). Dramatically, this is the murder scene; musically, it is one huge orchestral crescendo on the pitch B3. See if you can pick out some of the successively entering instruments, and then scroll down for the answer.
https://open.spotify.com/track/32FLHdpetPyACpyuOM6tIY?si=8NgaX-_jR4O9DT9_Zw2Msw
This reduction sets out the process:

In a landmark book about sound spectra, Robert Cogan described the beginning of this passage as "almost entirely fundamental": that is, almost a pure sine wave, with strictly minimized upper partials. We begin pppp with the muted French horn: an entirely appropriate choice in that it has the least spectrally active sound available in the standard symphony orchestra and, partly by definition, also the most distant one. Not only do the players sit near the back, but their instrument projects the sound backwards, further increasing the distance and ensuring that the majority of the audience hears primarily wall-reflected sound. Between this and the use of a mute, a great deal of high-register spectral content is removed, leaving that nearly pure fundamental. The mute on the solo violin, which is next to enter, has a similar spectral-auditory effect. When the bass clarinet joins the sound, some higher spectra are introduced, though few, as the instrument is high in its range and produces only odd-numbered partials. What follows continues this crescendo not only of sound, but of instrument types and spectral content. Naturally, the heavy brass are last to enter, burnishing the end to this spectral progression with brilliance.
For timbrally nuanced melodies
Finally, many composers since around 1900 have used timbral variation to create a kind of "kaleidoscope" melody. This is most commonly known as Klangfarbenmelodie ("sound-color melody"). The term Klangfarbenmelodie was coined by Schoenberg in his Harmonielehre (1911) and employed most notably in his "Farben" (no. 3 from Five Orchestral Pieces). It is also related to musical pointillism, in which one melody passes among many instruments to color a single line. Examples include Webern’s iconic Konzert, Op. 24, in which timbre helps to articulate the structural divisions of the row (about this, see this chapter), but also in a great deal of Mahler. See, for instance, this example from the beginning of Mahler 7/iii, in which a pointillist start begins to coalesce.
We’ll end this chapter with an extraordinary example: Webern’s orchestration of Bach’s Ricercata from the Musical Offering. The work is at once a faithful, note-for-note transcription of the original and an analysis-by-orchestration of its motives and melodic contour. It is more of a compositional orchestration than an arrangement or transcription per se. The image below provides a reduction of the exposition. There is a staff for each presentation of the theme (corresponding to the six entrances of the fugal voices).
Webern’s instrumental distribution of the fugal subject theme follows a palindromic, possibly even double palindromic design. Dotted lines beneath each staff demonstrate the first, primary, clear and consistent palindrome; those over the top set out the second, which is not so consistently used, and which may be less effective in accounting for the last two instrumental choices than the square brackets that illuminate how these two instruments often repeat an earlier pairing. The asterisks above the staff indicate notes doubled by the harp, the first of which serves to articulate the first timbral recurrence (initiating the palindrome), while the latter two identify the end of the theme. The diagonal arrows further speculate on the possible relation between the successive instrumental timbres of the first answer and those that begin the next two subject-answer statements.
Finally, the last two systems show how Sofia Gubaidulina’s violin concerto Offertorium takes up this double palindromic instrumentation of Bach’s theme. That timbral design is not consistent throughout (hence only presenting the first two instances of the theme), but instead relates to an overall formal process that truncates one note from the beginning and end of the theme at each successive presentation. This continues up to a central point, after which the process is symmetrically reversed.
https://open.spotify.com/track/4NgIfVEcWGKio97hyJQpp0?si=aUUcZC__TdynJgv1zuo4wA
Clearly these are highly specific modernist examples in which symmetry is paramount, but again, we can see pre-echoes of this kind of idea in pre-20th-century music. For instance, there are symmetrical timbral schemes in:
- Schubert 8/ii: the melody moves from the clarinet (in minor) to oboe (major) in the exposition; the process is reversed in the recapitulation (oboe-clarinet).
- Brahms 3/iii: the theme and accompaniment move from strings to winds in the first section and from winds to strings in the reprise.
Both cases reflect their larger forms just as Webern and Gubaidulina do.
- Coming soon!
A 7̂ that is one half step below 1̂. The leading tone is diatonic in major keys, but requires an accidental in minor keys.
Altered dominant chords
Altered dominant chords feature either an augmented or diminished fifth. Augmented fifths are indicated in analysis by “+” beside the Roman numeral. Diminished fifths are indicated by a “o” beside the Roman numeral.
Dominant with an augmented fifth
If you raise the fifth of a dominant triad, it will become an augmented triad. Typically, raised fifths resolve upward by step to the third of its target chord. Note that the augmented triad is a symmetrical chord than can be interpreted in multiple ways, making it difficult to identify its root without proper surrounding context. Like the diminished-seventh chord, this means that the augmented triad can be a pathway to distant, chromatic modulations. See Example 1, which shows the three possible enharmonic interpretations and resolutions of the C augmented triad.
Importantly, these chords do not resolve easily to minor triads, since the augmented fifth would not be able to resolve upward by step.
Example 1: The three possible resolutions of the C augmented triad.
The Dominant with Diminished Fifth
When you add a 7th to a Vo chord, you get a chord that sounds precisely like a French augmented-sixth chord. This equivalence becomes even clearer when you use the Vo7 chord in second inversion, leaving the lowered fifth in the bass voice to resolve downward by step. As Example 2 shows, the chords Vo4/3/V and the French augmented-sixth chord are identical.
Example 2: The dominant chord with a diminished fifth, and its equivalence with the French augmented-sixth chord.
Extended dominant chords
Extensions can be added to dominant chords to create new and interesting sonorities. These chords are typically found only in root position.
When composing these chords in a four-voice texture, you need to decide which notes to leave out. These chords will always include the root and the chordal seventh.
The V9 chord replaces a doubled root with a ninth. The ninth should resolve down by step.
The V11 chord replaces the third with an eleventh. The eleventh “resolves” by common-tone. This chord typically includes both the ninth and the eleventh, and resembles a IV chord with scale-degree 5 in the bass.
The V13 chord replaces the fifth with a thirteenth. The thirteenth “resolves” by leaping down by third to scale-degree 1.
- Coming soon!

