I. Fundamentals
18 Seventh Chords
Chelsey Hamm
Key Takeaways
- A seventh chord is a four-note chord whose notes can be arranged in thirds. A seventh chord can always be “stacked” so that its notes are either on all lines or all spaces.
- When a seventh chord is stacked in thirds, the lowest note is called the root, the lower middle note is called the third, the upper middle note is called the fifth, and the highest note is called the seventh, which is sometimes called the “chordal” seventh to distinguish it from the seventh scale degree.
- There are five common qualities of seventh chord. These qualities are the major-major seventh chord, major-minor seventh chord, minor-minor seventh chord, half-diminished seventh chord, and fully diminished seventh chord.
- There is another common way of naming seventh chords: the major-major seventh chord is also often called the major seventh chord, the major-minor seventh chord is also often called the dominant seventh chord, the minor-minor seventh chord is also often called the minor seventh chord, and the fully diminished seventh chord is also often simply called the diminished seventh chord.
- Within major and minor keys, seventh chords have particular qualities that correspond to scale degrees. These are the same in every major and minor key, which makes memorizing them useful.
- Seventh chords are identified by their root, quality of triad and seventh, and inversion.
In this chapter, we will focus on seventh chords: four-note chords whose notes can be stacked into thirds.
Seventh Chords
Like triads, the notes of a seventh chord can always be arranged in thirds, on adjacent lines or spaces of the staff. If a triad in closed spacing looks like a snowperson, then a seventh chord in closed spacing (as in the second measure of Example 1) looks like an extra-long snowperson, with a bottom, two middles, and a head.
https://musescore.com/user/32728834/scores/6843767/embed
Example 1. A seventh chord written melodically and harmonically.
Like in a triad, the lowest note of a seventh chord stacked in closed spacing is called the root, and the other notes are named for their generic intervals above the root, as shown in Example 2: the third, the fifth, and the seventh.
Seventh Chord Qualities and Nomenclature
Example 3 lists the five most common qualities of seventh chord: major-major, major-minor, minor-minor, half-diminished, and fully diminished. These qualities are determined by two factors:
- The quality of the triad created by the root, third, and fifth (shown in the second column)
- The quality of the seventh from the root to the seventh (shown in the third column)
A chord symbol for a seventh chord begins with the letter name of the triad’s root followed by an indication of the quality of its triad and seventh. Examples of chord symbols for different seventh chord qualities are given in the last column of Example 3.[1]
[table “73” not found /]
Example 3. Summary of nomenclature for different qualities of seventh chord.
For the first three qualities of seventh chord, the first word describes the quality of the triad, and the second word describes the quality of the seventh:
- major-major seventh chord = major triad + major seventh
- major-minor seventh chord = major triad + minor seventh
- minor-minor seventh chord = minor triad + minor seventh
The other two qualities are both built on diminished triads but differ in the quality of the seventh:
- half-diminished seventh chord (diminished triad, minor seventh)
- fully diminished seventh chord (diminished triad, diminished seventh)
Music theorists often use the names described above, but there is also another common way of naming these chords, given in parentheses in the first column of Example 3:
- The major-major seventh chord is also often called the major seventh chord.
- The major-minor seventh chord is also often called the dominant seventh chord.
- The minor-minor seventh chord is also often called the minor seventh chord.
- The fully diminished seventh chord is also often simply called the diminished seventh chord.
- The half-diminished seventh chord does not typically have an alternate name.
Your instructor may have you label these chords using one set of terminology or the other, or a mix of both.
Example 4 summarizes all this information in music notation.
https://musescore.com/user/32728834/scores/6850641/embed
Example 4. The qualities of sevenths and triads in various seventh chord types.
Don’t forget that when the root of a seventh chord has an accidental, you add that accidental into its name. For example, B♭mi7 is the chord symbol for a seventh chord with a B♭ minor triad and a minor seventh. Likewise, a G♯ma7 is the chord symbol for a seventh chord with a G♯ major triad and a major seventh.
In chord-symbol notation, if a pitch class other than the chord’s root is the lowest note in a seventh chord, then a slash is added, followed by a capital letter denoting the pitch class in the bass (lowest) voice. Example 5 shows a G half-diminished seventh chord (G∅7). In the first measure, the chord appears in first position; in the second measure, the chord’s seventh (F) is in the bass voice, so the chord symbol is written as G∅7/F. This topic will be explored more in the chapter Inversion and Figured Bass.
https://musescore.com/user/32728834/scores/6843772/embed
Example 5. Two seventh chords.
Listening to Seventh Chords
Listen carefully to the different qualities of seventh chord in Example 4. It is common to pair expressive qualities with seventh chords when learning what they sound like. You might think of major-major seventh chords as sounding “happy and jazzy,” major-minor seventh chords as sounding “unresolved” (like they strongly need to move to another chord), minor-minor seventh chords as “sad and jazzy,” half-diminished seventh chords as “scary and jazzy,” and fully diminished seventh chords as “very scary.”
Seventh Chord Qualities in Major and Minor
Seventh chords can be built on any note of the major scale. As you can see in Example 6, which is in the key of G major, seventh chords built on do [latex](\hat1)[/latex] and fa [latex](\hat4)[/latex] have a major triad and a major seventh, while seventh chords built on sol [latex](\hat5)[/latex] have a a major triad and a minor seventh (a dominant seventh chord). Seventh chords built on re, mi, and la [latex](\hat2,\ \hat3,[/latex] and [latex]\hat6)[/latex] have a minor triad and a minor seventh, while seventh chords built on ti [latex](\hat7)[/latex] are half-diminished—they have a diminished triad and a minor seventh. These seventh chord qualities do not change in different keys; consequently, memorizing these qualities can be very useful.
https://musescore.com/user/32728834/scores/8514077/embed
Example 6. Qualities of seventh chords in major keys.
Seventh chords can also be built on any note of the minor scale. Example 7, which is in the key of G minor, contains only one seventh chord built on sol [latex](\hat5)[/latex] and one on ti [latex](\hat7)[/latex]. It is common for these seventh chords to contain the raised leading tone—ti instead of te [latex](\hat7[/latex] instead of [latex]\downarrow\hat7)[/latex]. In Example 7, seventh chords built on do and fa [latex](\hat1[/latex] and [latex]\hat4)[/latex] have a minor triad and a minor seventh, while seventh chords build on sol [latex](\hat5)[/latex] with the raised leading tone have a major triad and a minor seventh (a dominant seventh chord). Seventh chords built on me and le [latex](\downarrow\hat3[/latex] and [latex]\downarrow\hat6)[/latex] have a major triad and a major seventh, while those built on re [latex](\hat2)[/latex] are half-diminished (containing a diminished triad and a minor seventh), and those built on ti [latex](\hat7)[/latex] are fully diminished (containing a diminished triad and a diminished seventh).
https://musescore.com/user/32728834/scores/6843776/embed
Example 8. Qualities of seventh chords in minor keys.
Spelling Seventh Chords
To build a seventh chord from a chord symbol, you need to be aware of its root and quality—inversion is discussed in the next chapter, titled Inversion and Figured Bass. The steps for spelling a seventh chord are similar to the steps for drawing a triad. Let’s start with spelling a major-major seventh chord:
- Draw the root on the staff.
- Draw notes a third, fifth, and seventh above the root (i.e., draw an “extra-long” snowperson).
- Think of (or write down) the major key signature of the triad’s root.
- Write any accidentals from the key signature that apply to the notes in the chord, creating a major triad and a major seventh.
For any other quality of seventh chord, add additional accidentals to alter the chord’s third, fifth, and/or seventh when appropriate.
Example 8 shows this process for a D major-major seventh chord (Dma7):
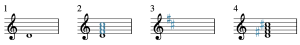
- The note D, the chord’s root, is drawn on the staff.
- An extra-long snowperson is drawn—an F, A, and C, the notes a generic third, fifth, and seventh above the D.
- The key signature of D major has been recalled. D major has two sharps, F♯ and C♯.
- Sharps (♯) have been added to the left of the F and the C, because F♯ and C♯ are in the key signature of D major.
The quality of the next chord will require us to write additional accidentals, so the process has a couple more steps. Example 9 shows the process for an A♭ fully diminished seventh chord (A♭o7):
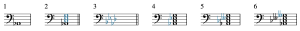
- The note A♭ is written because it is the root of the triad.
- An extra-long snowperson is drawn: C, E, and G are added because they are a generic third, fifth, and seventh, respectively, above A♭.
- The key signature of A♭ major is recalled. A♭ major has four flats: B♭, E♭, A♭, and D♭.
- E♭ is added, because it is in the key signature of A♭ major.
- We have now followed the process to spell a major-major seventh chord, but we want a fully diminished seventh chord, which means adding accidentals that are not in the key signature of A♭ major:
- C and E♭ are lowered by a half step to C♭ and E𝄫 to change the triad from major to diminished.
- To change the chord’s seventh from major to diminished, it needs to be lowered by two half steps, from G to G𝄫.
Following these steps is a reliable way for beginners to spell seventh chords, but it’s a time-consuming process. If you practice playing all of the qualities of seventh chords on an instrument until you are fluent in them, your knowledge of these notes will become more automatic without using this process.
Identifying Seventh Chords, Doubling, and Spacing
Like triads, seventh chords are also identified according to their root, quality, and inversion; inversion is discussed in the Inversion and Figured Bass chapter, so the examples here will be in root position.
- Identify and write its root.
- Imagine the major key signature of its root.
- Identify and write its quality of its triad.
- Identify and write its quality of its seventh.
Example 10 shows a seventh chord in root position for the process of identification.
https://musescore.com/user/32728834/scores/6843785/s/Ml4Mxs/embed
Example 10. A seventh chord in root position for identification.
To identify this seventh chord:
- Because the chord is in root position, the root is the lowest note, C♯.
- The key of C♯ major has seven sharps (every note is sharp). E and G would be sharp in the key of C♯ major, but we see that both of those notes are natural instead—lowered by a half step—making the triad diminished.
- The chord’s seventh, B, would also be sharp in C♯ major, but it is natural here. When a major seventh is made a half step smaller, it becomes a minor seventh.
- A diminished triad and a minor seventh form a half-diminished seventh chord; therefore, this is a C♯ half-diminished seventh chord (C♯∅7).
If the bottom note of a seventh chord has an imaginary key signature (because there is a double accidental that applies to it), use enharmonic equivalence to respell the seventh chord, following the process outlined in the last section of the Intervals chapter.
Like with triads, a seventh chord’s identification is not affected by the doubling of notes or open spacing of notes (even across multiple clefs). Example 11 shows two different seventh chords in [pb_glossary open spacing with doublings. Simply imagine or write the notes of seventh chords in closed spacing without any doublings to identify these chords, as we did previously.
https://musescore.com/user/32728834/scores/6843788/embed
Example 11. Two seventh chords with doublings in open spacing.
- Seventh Chords (musictheory.net)
- Understanding Seventh Chords in Music (Hello Music Theory)
- Introduction to Seventh Chords (Robert Hutchinson)
- Seventh Chords (Kaitlin Bove)
- Seventh Chords (Music Theory Academy)
- Seventh Chords (Carleton College)
- Seventh Chords For Dummies (YouTube)
- Seventh Chords – Music Theory Crash Course (YouTube)
- Seventh Chord Ear Training (teoria)
- Chord Ear Training (musictheory.net)
- Chord Ear Training (Tone Savvy)
- Seventh Chord Construction (.pdf, .pdf), p. 1 .pdf)
- Constructing and Identifying Seventh Chords (.pdf)
- Identifying Root Position Diatonic Seventh Chords, Major, p.1 (.pdf)
- Identifying Root Position Diatonic Seventh Chords, Minor, p.1 (.pdf)
- Seventh Chords Assignment #1 (.pdf, .mcsz)
- Seventh Chords Assignment #2 (.pdf, .mcsz)
- Seventh Chords Assignment #3 (.pdf, .mcsz)
- These chord symbols reflect those used in Open Music Theory, but you may come across others in your studies. See Chord Symbols for a more thorough explanation of these variations. ↵
The omnibus progression is a special type of chromatic sequence in which the bass and another voice in the texture move in contrary motion. Most commonly, the omnibus progression is used to prolong dominant harmony, but it can also be used as a means of modulating into distant keys.
Example 1 shows the prolongation of a dominant-seventh chord via a voice-exchange between the leading tone (in the soprano) and the root of the chord (in the bass).
Example 1. The omnibus progression prolongs dominant harmony using a chromatic a voice exchange between the leading tone and the root.
Notice that the voice leading in this progression is as smooth as possible: The only voices that are moving are the ones involved in the voice exchange. The other voices remain static as common tones.
The harmony throughout the
There are two ways of writing an omnibus progression: with the bass and upper voices converging, or with the bass and upper voices diverging.
The converging omnibus progression begins on a root-position dominant-seventh chord. The bass moves up- ward by semitone, while the voice with the leading tone moves downward by semitone, creating a voice ex- change. The remaining two upper voices maintain common tones.
Moving three semitones in this fashion brings you to another root-position dominant-seventh chord. Moving four semitones in this fashion brings you to the same dominant-seventh chord on which you began the progression, but this time, in first inversion.
The omnibus progression can be used to move into distant keys (and eventually traverse the octave) if, once you reach the new root-position dominant-seventh chord (that you arrived at after three semitones), you find the new leading tone and begin the process again.
The diverging omnibus progression works almost identically, but instead of moving the leading tone in contrary motion to the bass, you move the seventh. To move into distant keys, find the new seventh in the root-position dominant-seventh chord and repeat the process.
- Coming soon!
.front-matter h6 {
font-size: 1.25em;
}
.textbox--sidebar {
float: right;
margin: 1em 0 1em 1em;
max-width: 45%;
}
.textbox.textbox--key-takeaways .textbox__header p {
font: sans-serif !important;
font-weight: bold;
text-transform: uppercase;
font-style: normal;
font-size: larger;
}
a:link {
text-decoration: none;
}
button {
background: yellow;
}
Altered dominant chords
Altered dominant chords feature either an augmented or diminished fifth. Augmented fifths are indicated in analysis by “+” beside the Roman numeral. Diminished fifths are indicated by a “o” beside the Roman numeral.
Dominant with an augmented fifth
If you raise the fifth of a dominant triad, it will become an augmented triad. Typically, raised fifths resolve upward by step to the third of its target chord. Note that the augmented triad is a symmetrical chord than can be interpreted in multiple ways, making it difficult to identify its root without proper surrounding context. Like the diminished-seventh chord, this means that the augmented triad can be a pathway to distant, chromatic modulations. See Example 1, which shows the three possible enharmonic interpretations and resolutions of the C augmented triad.
Importantly, these chords do not resolve easily to minor triads, since the augmented fifth would not be able to resolve upward by step.
Example 1: The three possible resolutions of the C augmented triad.
The Dominant with Diminished Fifth
When you add a 7th to a Vo chord, you get a chord that sounds precisely like a French augmented-sixth chord. This equivalence becomes even clearer when you use the Vo7 chord in second inversion, leaving the lowered fifth in the bass voice to resolve downward by step. As Example 2 shows, the chords Vo4/3/V and the French augmented-sixth chord are identical.
Example 2: The dominant chord with a diminished fifth, and its equivalence with the French augmented-sixth chord.
Extended dominant chords
Extensions can be added to dominant chords to create new and interesting sonorities. These chords are typically found only in root position.
When composing these chords in a four-voice texture, you need to decide which notes to leave out. These chords will always include the root and the chordal seventh.
The V9 chord replaces a doubled root with a ninth. The ninth should resolve down by step.
The V11 chord replaces the third with an eleventh. The eleventh “resolves” by common-tone. This chord typically includes both the ninth and the eleventh, and resembles a IV chord with scale-degree 5 in the bass.
The V13 chord replaces the fifth with a thirteenth. The thirteenth “resolves” by leaping down by third to scale-degree 1.
- Coming soon!
Key Takeaways
- The iii chord (III in minor) is a weak predominant that typically moves through a strong predominant on the way to a V chord.
- In major, iii usually harmonizes a descending ti [latex](\hat7)[/latex]; similarly, in minor, III usually harmonizes a descending te [latex](\downarrow\hat7)[/latex].
- iii/III is usually found in root position.
- iii is not used as a substitute for I6 (see the explanation below Example 1).
- iii is not not a very common chord.
Overview: the iii chord
It’s most common for mi ([latex]\hat{3}[/latex]) in the bass to be harmonized with a I6 chord. Occasionally, however, composers choose to use iii rather than I6 (Example 1). The iii chord is used in one relatively specific situation: after a I chord, harmonizing a descending ti/te [latex](\hat7/\downarrow\hat7)[/latex] in an upper voice. It commonly moves to to a strong predominant, though it can move directly to V in a bass arpeggiation do–mi–sol [latex](\hat1-\hat3-\hat5)[/latex] harmonized I–iii–V, and is usually in root position.
Example 1. The iii chord in Koji Kondo's Athletic Theme from Super Mario 3 (4:19–4:24).
It's important to emphasize that iii isn't simply a substitute for I6 in Western classical music. For instance, in an earlier chapter on tonic prolongations, we saw that the bass line do–re–mi [latex](\hat1-\hat2-\hat3)[/latex] is commonly harmonized with [latex]\mathrm{I-V^4_3-I^6}[/latex]. Composers don't use [latex]\mathrm{I-V^4_3-iii}[/latex] as an alternative. That's because iii functions like vi, as a weak predominant that most often travels through a strong predominant to get to V. The progression [latex]\mathrm{I-V^4_3-iii}[/latex] shows the opposite: V getting to iii, which isn't stylistically normative. Finally, keep in mind that iii does not appear very often in common-practice tonality, so it should be used sparingly.
Writing with iii
Example 2 shows the voice leading for the most common use of iii: as a weak predominant that moves through a strong predominant on its way to V. In the major-mode progressions (Examples 2a and 2b), notice that the leading tone descends to la [latex](\hat{6})[/latex] when iii moves to the predominant.
In the minor-mode progressions (Examples 2c and 2d), te [latex](\downarrow\hat{7})[/latex] descends to le [latex](\downarrow\hat{6})[/latex] when III moves to a predominant. Notice that III involves te [latex](\downarrow\hat{7})[/latex], not ti [latex](\uparrow\hat{7})[/latex]. That is, III is major, not augmented, which is what would happen if we used ti [latex](\uparrow\hat{7})[/latex].
Example 2. Writing with iii going to a strong predominant.
Example 3 shows that iii can also go directly to V. Note that this progression doesn't work well in minor, since III contains te [latex](\downarrow\hat{7})[/latex] but V contains ti [latex](\uparrow\hat{7})[/latex], and the immediate juxtaposition of these two scale degrees is not stylistic for Western classical music.
Example 3. Writing with iii going to V.
The previous chapters have introduced species counterpoint and the iconic pedagogical treatise on cantus firmus composition, Johann Joseph Fux's Gradus ad Parnassum (1725). This page provides the full cantus firmus exercises of that treatise so you can try your hand at species counterpoint à la Fux.
Gradus ad Parnassum is in three sections:
- Two Voices (46 exercises)
- Three Voices (44 exercises)
- Four Voices (32 exercises)
For each of these sections, we provide four files:
- Exercises: all of the cantus firmus exercises with only the cantus firmus present and the other part(s) left blank for you to complete.
- Solutions: all of Fux’s solutions to those exercises—i.e., both the cantus firmus and the additional part(s) that Fux wrote as answers.
- Annotations: Those solutions annotated with the interval that every note in each additional part forms with the cantus firmus part.
- Distinct: Every distinct cantus firmus in all parts. All of the exercises are based on this format, so these simple files distill all possibilities: you can use this file to do any species exercise, on any cantus firmus, in any part arrangement.
Everything is provided in an editable format so teachers can adjust and combine exercises freely for their own classes’ needs. Specifically, the files are provided in the following formats:
- .mxl: open these in any music notation package like MuseScore, Sibelius, or Finale
- .mscz: for MuseScore specifically, preserving all original formatting
View Online and/or Download
View these files on MuseScore.com (and download in multiple formats if you have an account):
- The "Annotations" files on OMT's MuseScore page
- All of the files on Four Score and More's MuseScore page
Click on the links to download any particular type. Please note that the .mxl files are hosted externally on http://fourscoreandmore.org/species/, so you will be redirected and may prefer to open in a new tab.
| Part | Exercises | Solutions | Annotated | Distinct |
|---|---|---|---|---|
| I | .mxl, .mscz, |
.mxl, .mscz, |
.mxl, .mscz, |
.mxl, .mscz, |
| II | .mxl, .mscz, |
.mxl, .mscz, |
.mxl, .mscz, |
.mxl, .mscz, |
| III | .mxl, .mscz, |
.mxl, .mscz, |
.mxl, .mscz, |
.mxl, .mscz, |
Gradus ad Parnassum Data
Each exercise includes the following information:
- Figure number (in the modern Norton/Mann edition, 1965)
- Species type
- Modal final
- Cantus firmus part
For ease of reference, the following subsections and tables set out that information in full.
Finally, a note on clefs. These files use the clefs in the Norton/Mann edition (1965) for parts I and II. Part III keeps the same clefs throughout to be consistent both internally and with the modern choral score layout (treble, treble, treble 8vb, bass). Teachers may wish to choose their own clefs as part of adapting these files for class.
Part I (Two Voices)
[table “77” not found /]
Fux basically uses one cantus firmus for each modal final throughout. The note sequences are as follows, along with their usage counts (46 total) and the minor exceptions:
| Modal final | Pitches | Number of times used, and exceptions |
|---|---|---|
| D | D4–F4–E4–D4–G4–F4–A4–G4–F4–E4–D4 | 10 counts |
| E | E4–C4–D4–C4–A3–A4–G4–E4–F4–E4 | 10 counts |
| F | F3–G3–A3–F3–D3–E3–F3–C4–A3–F3–G3–F3 | 10 counts including one at the octave above, (fig. 13: starting F4) |
| G | G3–C4–B3–G3–C4–E4–D4–G4–E4–C4–D4–B3–A3–G3 | 6 counts |
| A | A3–C4–B3–D4–C4–E4–F4–E4–D4–C4–B3–A3 | 6 counts including one lacking the first D (fig. 42: A3–C4–B3–C4–E4 ...) |
| C | C4–E4–F4–G4–E4–A4–G4–E4–F4–E4–D4–C4 | 2 counts; the most anomalous case |
| C | C4–D4–F4–E4–G4–E4–F4–E4–D4–C4 | 2 counts; more divergent than for the other modes |
Part II (Three Voices)
[table “78” not found /]
The table below summarizes the cantus firmi used in Part II:
| Modal final | Pitches | Number of times used, and exceptions |
|---|---|---|
| D | D4–F4–E4–D4–G4–F4–A4–G4–F4–E4–D4 | 16 counts at two octaves (D3 and D4) |
| E | E4–C4–D4–C4–A3–A4–G4–E4–F4–E4 | 12 counts at two octaves (E3 and E4) |
| F | F3–G3–A3–F3–D3–E3–F3–C4–A3–F3–G3–F3 | 9 counts at two octaves (F3 and F4) |
| G | G3–C4–B3–G3–C4–E4–D4–G4–E4–C4–D4–B3–A3–G3 | 2 counts |
| A | A3–C4–B3–D4–C4–E4–F4–E4–D4–C4–B3–A3 | 3 counts at three octaves (A2, A3 and A4) |
| C | C4–E4–F4–G4–E4–A4–G4–E4–F4–E4–D4–C4 | 2 counts; corresponds to the first case for Part I |
Part III (Four Voices)
[table “79” not found /]
The table below summarizes the cantus firmi used in Part III:
| Modal final | Pitches | Number of times used, and exceptions |
|---|---|---|
| D | D4–F4–E4–D4–G4–F4–A4–G4–F4–E4–D4 | 21 counts at two octaves (D3 and D4) |
| E | E4–C4–D4–C4–A3–A4–G4–E4–F4–E4 | 7 counts, one at E5 (fig. 184) |
| F | F3–G3–A3–F3–D3–E3–F3–C4–A3–F3–G3–F3 | 4 counts at two octaves (F3 and F4) |
- Fux, Johann Joseph. (1725) 1965. Gradus ad Parnassum. Translated and edited by Alfred Mann. New York: W. W. Norton.
Key Takeaways
We begin with an at-a-glance summary of some important schemas, then proceed to set out each of the schemas listed one by one.
Overall Short Summary
Musical notation
Here are files in musical notation with all the schemas listed on this page:
These files provide a set of schemas, with the constituent parts set out as prototypically as is possible in musical notation: that is, with melody and figured bass lines, along with (in the first file's case) chords in a middle part realizing those figures. Musical notation is obviously useful, though really, schemas are prototypes that exist apart from any specific realization, so the more abstract representations in tables and the like are better in some ways. That's why you'll see them set out in this fashion here and in other literature on this topic.
Summarizing table
[table “75” not found /]
Itemized List
Opening Gambits
Romanesca
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | S | W | S | W |
| Melody | do [latex]\hat1[/latex] |
sol [latex]\hat5[/latex] |
do [latex]\hat1[/latex] |
do [latex]\hat1[/latex] |
| Bass | do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
la [latex]\hat6[/latex] |
mi [latex]\hat3[/latex] |
| Figures | 5 | 6 | 5 | 6 |
| Roman numerals | I | V | vi | I |
Do–Re–Mi
| Stage | 1 | 2 | 3 |
|---|---|---|---|
| Meter | S | W | S |
| Melody | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
mi [latex]\hat3[/latex] |
| Bass | do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 6 | 5 |
| Roman numerals | I | V | I |
Many of the schemas involve two steps that can be considered schemas on their own. These often take the form of question-answer pairs.
Here, we have the Do–Re opening part as the opening question:
| Stage | 1 | 2 |
|---|---|---|
| Meter | S | W |
| Melody | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
| Bass | do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
| Figures | 5 | 6 |
| Roman numerals | I | V |
That Do–Re is answered by the Re–Mi:
| Stage | 1 | 2 |
|---|---|---|
| Meter | W | S |
| Melody | re [latex]\hat2[/latex] |
mi [latex]\hat3[/latex] |
| Bass | ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6 | 5 |
| Roman numerals | V | I |
The Do–Re–Mi may also appear in a four-stage version by putting those constituent parts back together. This basically involves doubling up the central stage of the three-stage version.
Sol–Fa–Mi
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | sol [latex]\hat5[/latex] |
fa [latex]\hat4[/latex] |
fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 5 | 6/5 | 5 |
| Roman numerals | I | ii | V | I |
Again, this comprises two parts.
Opening part (Sol–Fa):
| Stage | 1 | 2 |
|---|---|---|
| Meter | W | S |
| Melody | sol [latex]\hat5[/latex] |
fa [latex]\hat4[/latex] |
| Bass | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
| Figures | 5 | 5 |
| Roman numerals | I | ii |
Answering part (Fa–Mi):
| Stage | 1 | 2 |
|---|---|---|
| Meter | W | S |
| Melody | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6 | 5 |
| Roman numerals | V | I |
This schema may also appear with the harmony slightly altered, as follows:
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | sol [latex]\hat5[/latex] |
fa [latex]\hat4[/latex] |
fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 6 | 6/5 | 5 |
| Roman numerals | I | vii | V | I |
Meyer
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 6/4/3 | 6/5 | 5 |
| Roman numerals | I | V | V | I |
Opening part:
| Stage | 1 | 2 |
|---|---|---|
| Meter | W | S |
| Melody | do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
| Bass | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
| Figures | 5 | 6,4,3 |
| Roman numerals | I | V |
Closing part:
| Stage | 1 | 2 |
|---|---|---|
| Meter | W | S |
| Melody | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6,5 | 5 |
| Roman numerals | V | I |
Aprile
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | S | W | S | W |
| Melody | do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
| Bass | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 6,4,3 | 6,5 | 5 |
| Roman numerals | I | V | V | I |
Jupiter
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | S | W | S | W |
| Melody | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
sol [latex]\hat5[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 6 | 5 | 5 |
| Roman numerals | I | V | V | I |
Pastorella
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | S | W | S | W |
| Melody | mi [latex]\hat3[/latex] |
re [latex]\hat2[/latex] |
fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | do [latex]\hat1[/latex] |
sol [latex]\hat5[/latex] |
sol [latex]\hat5[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 5 | 7 | 5 |
| Roman numerals | I | V | V | I |
Answer/Process/Transition
Prinner and Modulating Prinner
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | S | W | S | W |
| Melody | la [latex]\hat6[/latex] |
sol [latex]\hat5[/latex] |
fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 6 | 7-6 | I |
| Roman numerals | IV | I | vii | I |
A slight variant on this inserts a root-position dominant before the final stage:
| Stage | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Meter | S | W | S | W | S |
| Melody | la [latex]\hat6[/latex] |
sol [latex]\hat5[/latex] |
fa [latex]\hat4[/latex] |
fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
re [latex]\hat2[/latex] |
sol [latex]\hat5[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 6 | 7–6 | 7 | 5 |
| Roman numerals | IV | I | vii | V | I |
The Prinner can also be used to modulate from the tonic to the dominant. This variant is called the Modulating Prinner:
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | S | W | S | W |
| Melody | mi [latex]\hat3[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
| Bass | do [latex]\hat8[/latex] |
ti [latex]\hat7[/latex] |
la [latex]\hat6[/latex] |
sol [latex]\hat5[/latex] |
| Figures | 5 | 6 | 7-♯6 | 5 |
| Roman numerals | I | V | vii/V | V |
Again, this can come with an additional root-position dominant:
| Stage | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Meter | S | W | S | W | S |
| Melody | mi [latex]\hat3[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
| Bass | do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
la [latex]\hat6[/latex] |
re [latex]\hat2[/latex] |
sol [latex]\hat5[/latex] |
| Figures | 5 | 6 | 7–♯6 | 7/♯ | 5 |
| Roman numerals | I | V | vii/V | V/V | V |
Fonte
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | sol [latex]\hat5[/latex] |
fa [latex]\hat4[/latex] |
fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | di [latex]\uparrow\hat1[/latex] |
re [latex]\hat2[/latex] |
ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6/5 | 5 | 6/5 | 5 |
| Roman numerals | V/ii | ii | V | I |
The Fonte has a strong relation to the Meyer and indeed to the cycle of fifths. This effectively tonicizes the A minor key (e.g., the supertonic minor) and then a major key a tone below (the overall tonic). The modular part is just one of those tonicizations:
| Stage | 1 | 2 |
|---|---|---|
| Meter | W | S |
| Melody | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6/5 | 5/3 |
| Roman numerals | V | I |
Monte
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | do-te [latex]\hat1-\downarrow\hat7[/latex] |
la [latex]\hat6[/latex] |
re-do [latex]\hat2-\hat1[/latex] |
ti [latex]\hat7[/latex] |
| Bass | mi [latex]\hat3[/latex] |
fa [latex]\hat4[/latex] |
fi [latex]\uparrow\hat4[/latex] |
sol [latex]\hat5[/latex] |
| Figures | 6/5 | 5 | 6/5 | 5 |
| Roman numerals | V/IV | V | V/V | V |
Like the Fonte, the Monte also goes through two tonicizations with a sequential treatment of a modular half:
| Stage | 1 | 2 |
|---|---|---|
| Meter | W | S |
| Melody | sol-fa [latex]\hat5-\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6/5 | 5 |
| Roman numerals | V | I |
Ponte
| Stage | 1 | 2 | 3 |
|---|---|---|---|
| Meter | S | W | S |
| Melody | sol [latex]\hat5[/latex] |
ti [latex]\hat7[/latex] |
re [latex]\hat2[/latex] |
| Bass | sol [latex]\hat5[/latex] |
sol [latex]\hat5[/latex] |
sol [latex]\hat5[/latex] |
| Figures | 5 | 7 | 7 |
| Roman numerals | V | V | V |
Pre-Cadential / Incomplete Cadences
Fenaroli
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | S | W | S | W |
| Melody | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Bass | ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
mi [latex]\hat3[/latex] |
| Figures | 6/5 | 5 | 6/5 | 6 |
| Roman numerals | V | I | V | I |
Indugio
| Stage | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Meter | S | W | S | W | S |
| Melody | re [latex]\hat2[/latex] |
fa [latex]\hat4[/latex] |
la [latex]\hat6[/latex] |
do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
| Bass | fa [latex]\hat4[/latex] |
fa [latex]\hat4[/latex] |
fa [latex]\hat4[/latex] |
fi [latex]\uparrow\hat4[/latex] |
sol [latex]\hat5[/latex] |
| Figures | 6/5 | 6/5 | 6/5 | 6/5 | 5 |
| Roman numerals | IV | IV | IV | V/V | V |
Deceptive Cadence
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
| Bass | mi [latex]\hat3[/latex] |
fa [latex]\hat4[/latex] |
sol [latex]\hat5[/latex] |
la [latex]\hat6[/latex] |
| Figures | 6 | 6/5 | 5 | 5 |
| Roman numerals | I | ii | V | vi |
Evaded Cadence
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
| Bass | mi [latex]\hat3[/latex] |
fa [latex]\hat4[/latex] |
sol [latex]\hat5[/latex] |
mi [latex]\hat3[/latex] |
| Figures | 6 | 6/5 | 5 | 6 |
| Roman numerals | I | ii | V | I |
Passo Indietro
| Stage | 1 | 2 |
|---|---|---|
| Meter | S | W |
| Melody | ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Bass | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Figures | 6/4/2 | 6 |
| Roman numerals | V | I |
The Passo Indietro is essentially the first two stages of a Prinner. Literally a "stepping back," the Passo Indietro often precedes a significant cadence.
Comma
| Stage | 1 | 2 |
|---|---|---|
| Meter | W | S |
| Melody | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
| Bass | ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6/5 | 5 |
| Roman numerals | V | I |
Converging Cadence
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | mi [latex]\hat3[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
ti [latex]\hat7[/latex] |
| Bass | mi [latex]\hat3[/latex] |
fa [latex]\hat4[/latex] |
fi [latex]\uparrow\hat4[/latex] |
sol [latex]\hat5[/latex] |
| Figures | 6 | 6/5 | 6/5 | 5 |
| Roman numerals | I | ii | V/V | V |
This cadence is also known as the fa–fi–sol half cadence after the definitive bass line: [latex]\hat4-\uparrow\hat4-\hat5[/latex]. Note the correspondence between this schema and the Indugio.
Cadences and Post-Cadential
Cadenza Semplice
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
| Bass | mi [latex]\hat3[/latex] |
fa [latex]\hat4[/latex] |
sol [latex]\hat5[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6 | 6/5 | 5 | 5 |
| Roman numerals | I | ii | V | I |
Cadenza Composta
| Stage | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Meter | W | S | S | W | S |
| Melody | do [latex]\hat1[/latex] |
re [latex]\hat2[/latex] |
mi [latex]\hat3[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
| Bass | mi [latex]\hat3[/latex] |
fa [latex]\hat4[/latex] |
sol [latex]\hat5[/latex] |
sol [latex]\hat5[/latex] |
do [latex]\hat1[/latex] |
| Figures | 6 | 6/5 | 6/4 | 7 | 5 |
| Roman numerals | I | ii | Cad. | V | I |
Cadenza Doppia
| Stage | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Meter | S | W | S | W | S |
| Melody | fa [latex]\hat4[/latex] |
mi [latex]\hat3[/latex] |
re [latex]\hat2[/latex] |
re [latex]\hat2[/latex] |
do [latex]\hat1[/latex] |
| Bass | sol [latex]\hat5[/latex] |
sol [latex]\hat5[/latex] |
sol [latex]\hat5[/latex] |
sol [latex]\hat5[/latex] |
do [latex]\hat1[/latex] |
| Figures | 5 | 6/4 | 4 | 3 | 5 |
| Roman numerals | V | V | V | V | I |
Quiescenza
| Stage | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Meter | W | S | W | S |
| Melody | te [latex]\downarrow\hat7[/latex] |
la [latex]\hat6[/latex] |
ti [latex]\hat7[/latex] |
do [latex]\hat1[/latex] |
| Bass | do [latex]\hat1[/latex] |
do [latex]\hat1[/latex] |
do [latex]\hat1[/latex] |
do [latex]\hat1[/latex] |
| Figures | ♭7 | 6/4 | 7/4/2 | 5 |
| Roman numerals | V/IV | V | V | I |
The Quiescenza is a post-cadential schema.
A seventh chord in which the triad quality is diminished and the seventh quality is minor.
Key Takeaways
This chapter discusses harmonizations of the scale using the so-called "rule of the octave" and other sequential configurations. There are many files provided to view or download:
- The Rule of the Octave
- Harmonizing the scale with sequences
The Rule of the Octave
The "Rule of the Octave" is an important part of the schema/partimento tradition. You might like to think of it as a kind of cheat sheet for harmonizing bass lines: there's one chord for each scale degree, and you can go a long way by just matching up those bass notes with their corresponding chord.
There are many, subtly different versions of the Rule of the Octave harmonization. The version used here is closely based on that of Fedele Fenaroli (Naples, 1775), with just a couple of modifications to preserve a consistent number of voices throughout (four voices, including the bass) and to avoid any suggestion of parallels.
Approaching the "Rule" from parallel [latex]^6_3[/latex]s
File downloads: .mscz, .mxl, .pdf
Let's begin by building up our version of the Rule of the Octave from simple principles, starting with parallel [latex]^6_3[/latex] (first inversion) chords. You could also think of this as a matter of moving from a flat to a rich harmonic hierarchy, or else as a "Regolo recipe": how to make or understand the rule in four easy steps.
- We begin with a simple harmonization of the bass scale using parallel [latex]^6_3[/latex] chords only. There's nothing grammatically incorrect about this, but neither does it have much of a sense of hierarchy or variety. In short, it's not very interesting.
- Next we put in strategic [latex]^5_3[/latex]s on the first and last chords to give a sense of closure on the tonic.
- Then we also add a [latex]^5_3[/latex] on the dominant chords of both ascending and descending forms to further nuance the hierarchy (these are important chords too).
- Finally, we precede each of the tonic and dominant chords (including those in inversion) with seventh chords. In one case, this also involves a chromatic alteration for a stronger sense of tonicizing the dominant. Why do you think we might only make that change this one time, and not anywhere else in the progression?
Rule of the Octave from [latex]^6_3[/latex] by FourScoreAndMore
Examining the Rule part by part
File downloads: .mscz, .mxl, .pdf
Having arrived at the Rule, this second file deconstructs it again so you can practice and engage with it in parts, with any number of voices, and in any position (i.e., any inversion of the right-hand harmonization). Keep practicing each component part separately and in a range of keys to build fluency with and abstraction of the Rule. (Note: you can transpose scores in MuseScore with the Notes menu: Notes/Transpose.)
We begin by combining the bass scale with each of the three upper-voice parts in turn, centered respectively on the:
- tonic (first system of each page: ascending on p. 1; descending on p. 2)
- mediant (second system)
- dominant (third system)
These systems are annotated with the interval between the upper and lower parts.
We then combine those upper parts into three-note right-hand chords to generate the Rule.
Here the three versions ("positions" in Fenaroli’s language) are given by the inversion of the chord. Again, the top voice is centered successively on the:
- tonic (fourth system)
- mediant (fifth system)
- dominant (sixth system)
Rule of the Octave Part by Part by FourScoreAndMore
Harmonizing the Scale with Sequences
File Downloads and online:
- Open score (one voice per part): .mscz, .mxl, .pdf, link to view the score online
- Short (piano) score: .mscz, .mxl, .pdf, link to view the score online
Note: The open and short-score versions of this material are otherwise identical, so these introductory comments apply equally to both.
As we've seen above, the Rule of the Octave can be thought of as in terms of a sequential harmonization of bass scales (parallel [latex]^6_3[/latex] chords). This section looks at some other sequential harmonizations of the bass scale here. Basically, this involves patterns of one or more harmonies which repeat sequentially in the direction of the scale. Some of these work in the same way for both ascending and descending forms; others require some modification.
We begin just as we did before, with a simple harmonization of the scale using parallel [latex]^6_3[/latex] chords only. The following systems proceed to patterns of:
5–6 patterns
- Ascending: In the ascending form, we alternate between the fifth and sixth above each note of the bass line scale.
- Descending: In the descending form, we could do the same note-by-note alternation as the ascending form, or else alternate between the fifth and sixth on separate notes (as in this file).
7–6 patterns: chains of suspensions
- Ascending: 7–6 suspensions involve a descending upper part, so in the ascending form of this pattern, we need to add in a leap up the octave to restart the pattern, so the repeating pattern is more like 7–6–8.
- Descending: Here the descending sequence matches the descending scale, so no modification is necessary. We essentially go back to the parallel [latex]^6_3[/latex] chords we started with, and just delay or offset the top line.
Cycles of fifths
The cycle of fifths is a based on a progression of root motion descending by fifths. Hiding in this pattern is another (usually descending) scalic progression between alternate bass notes. This arises because instead of literally going down two fifths, we usually go down a fifth and up a fourth, which is the equivalent progression, just keeping it in the same register / octave. At the end of one such "down a fifth, up a fourth," we end up a step lower than where we started, and so we also have a stepwise progression that can be scalic (if it is diatonic—i.e., not modulating).
We set this out in some of the main forms:
- Descending 1: with triads only
- Descending 2: with sevenths and suspensions (cf. 7–6 descending)
- Descending 3: "zigzag" circle-of-fifths (note the outer-voice canon)
Finally, we set out one version of this in the ascending direction: - Ascending 1: with 4–3 suspensions
2–3: more chains of suspensions
So far, we've used 7–6 and 4–3 suspensions, so that leaves us one more important type: the 2–3 suspension (which is the inversion of 7–6).
- Ascending: Just like the 7–6 suspensions above, for the ascending scale, we need to restart each pattern, so it ends up being 2–3–1 with the upper part, or 9–8–10 with the bass.
- Descending: Again, no restart is needed for the descending form. The 2–3 pattern sets up a series of [latex]^4_2[/latex] to 6 progressions like the important V[latex]^4_2[/latex]–I6 progression, except that we've kept it diatonic here (i.e., without tonicizing each key).
Scale Sequences Short by FourScoreAndMore
The partimenti approach really calls for hands-on practice.
- Begin by playing through these examples from the files provided, preferably in a range of different keys. (Note: As mentioned above, you can transpose scores in MuseScore with the Notes menu: Notes/Transpose).
- See if you can memorize the patterns. Test yourself by:
- writing them out on paper (start with a blank scale)
- playing them from memory
- Both with the music and (when you're ready) from memory, try embellishing these basic patterns.
.front-matter h6 {
font-size: 1.25em;
}
.textbox--sidebar {
float: right;
margin: 1em 0 1em 1em;
max-width: 45%;
}
.textbox.textbox--key-takeaways .textbox__header p {
font: sans-serif !important;
font-weight: bold;
text-transform: uppercase;
font-style: normal;
font-size: larger;
}
a:link {
text-decoration: none;
}
.button {
background-color: ivory;
color: purple;
}
div.part-title {
color: var(--primary);
font: 700 1.25rem "FreeSans", sans-serif;
text-transform: uppercase !important;
}
A seventh chord in which the triad quality is major and the seventh quality is minor.
.front-matter h6 {
font-size: 1.25em;
}
.textbox--sidebar {
float: right;
margin: 1em 0 1em 1em;
max-width: 45%;
}
.textbox.textbox--key-takeaways .textbox__header p {
font: sans-serif !important;
font-weight: bold;
text-transform: uppercase;
font-style: normal;
font-size: large;
}
a:link {
text-decoration: none;
}
.button {
background-color: ivory;
color: purple;
}
div.part-title {
color: var(--primary);
font: 700 1.25rem "FreeSans", sans-serif;
text-transform: uppercase !important;
}
.front-matter h6 {
font-size: 1.25em;
}
.textbox--sidebar {
float: right;
margin: 1em 0 1em 1em;
max-width: 45%;
}
.textbox.textbox--key-takeaways .textbox__header p {
font: sans-serif !important;
font-weight: bold;
text-transform: uppercase;
font-style: normal;
font-size: x-large;
}
a:link {
text-decoration: none;
}
.button {
background-color: ivory;
color: purple;
}
div.part-title {
color: var(--primary);
font: 700 1.25rem "FreeSans", sans-serif;
text-transform: uppercase !important;
}
Key Takeaways
- where it came from: not only Schoenberg, but also Hauer and others
- what it’s "really" about: a new world order, and if so an equalising or totalising one?
- tonal precedents in Bach and Haydn, and "tonal tone rows" in (for example) Alban Berg, Hale Smith, and Benjamin Britten
- "total" or "integral" serialism in (for example) Ruth Crawford Seeger, Milton Babbitt, Olivier Messiaen, Karlheinz Stockhausen, Pierre Boulez.
Why Serialism? What’s the Attraction?
Some grand narratives of 20th-century music cast atonality as a logical consequence of a historical trend toward ever more chromaticism, and serialism as a matter of creating a radically different kind of structure out of the total chromatic. It would appear to achieve that end, at least for composers who joined Schoenberg in viewing it as a “method of composing with twelve tones which are related only with one another” (1950, 107)—contrast that with the fundamentally hierarchical tonal system. It may not be coincidental that it emerged in interwar Europe, when there may well have been a desire to start anew.
Equal tones? A new world order? Maybe, but the method has served a wide range of composers with correspondingly diverse aims, so it’s not so straightforward to summarize. There’s also a totalizing angle here that’s rather less utopian. Schoenberg is famously alleged to have described "his" discovery as one "which will ensure the supremacy of German music for the next hundred years" (qtd. in Stuckenschmidt 1977, 277). Schoenberg may or may not have actually said this, but Boulez definitely did later describe every composer to have remained "outside the serial experiments" since their discovery as "useless" ("Schönberg est mort," Score, 1952, reproduced in Notes of an Apprenticeship, 1968, 274).
A Series of Precedents?
There is a great deal of precedent for general forms of musical thinking pertinent to serial technique, from simple melodic inversion to furiously complex crab canons, and certain works like Bach’s Art of Fugue are notable partly for the strictness and comprehensiveness of design in general, and the healthy dose of "mirror writing" in particular.
In these cases, the mirror is usually "horizontal," giving versions of the twelve-tone technique’s I-form. The R-form of retrograde symmetry (given by a "vertical" mirror, if you will) is a primarily 20th-century concern, serial and otherwise. Non-serial 20th-century examples include a great deal of Bartók, the prelude/postlude pair in Hindemith's Ludus Tonalis, and Britten's Cantata Academica mvt. 2 (tellingly titled Alla rovescio). There are earlier examples, such as the Menuet al Roverso from Haydn’s Symphony no. 47 in G, but they are very rare.
There are (equally rare and also rather dubious) cases of tonal works that are said to exhibit the specifically twelve-tone practice of rotating through all the pitches. Often-cited examples include the choice of keys in the development of the finale to Mozart’s Symphony no. 40.
Conversely, there are 20th-century composers who wrote music that is serially organized in the sense that we would recognize, but in such a way as to embrace the sound world of an extended tonality (Example 1). Examples of this include:
- Alban Berg's Violin Concerto, with its row centered on triads and fifths.
- Hale Smith's Evocation, which the composer notes to have an "affinity" with jazz. Among the "jazzy" and/or "tonal" elements of this piece is the foregrounding of set [0,2,7], which the scholar Horace J. Maxile Jr. links to "the quartal harmonic and improvisational stylings of bop and post-bop schools" (2004, 125).
- Benjamin Britten’s Turn of the Screw, which adopts a similarly quartal structure in the row from which both the theme and tonal centers for the acts are serially organized.
Example 1. Tonal Tone Rows by FourScoreAndMore
Speaking of "tonal serialism," the trappings of tonality are not limited to pitch: what composers do with the other parameters is equally important. It's often observed (usually critically) that Schoenberg's early serial works may have used the twelve-tone technique in the pitch domain, but still adopted tonal forms, rhythms, and idioms such as waltzes.
The Emergence and Evolution of the Twelve-Tone Technique
Schoenberg is intimately associated with the twelve-tone technique and was quite content to describe it as "his" discovery (as above), though many people arrived at the idea largely independently around the same time, notably including Josef Matthias Hauer and Herbert Eimert. Schoenberg famously discussed relevant considerations like the "emancipation of the dissonance" early on, but his thoughts on serialism only emerged later, after those two others.
Hauer’s theory as expressed in his Zwölftontechnik: Die Lehre von den Tropen (1926) is notable for its early formalization of the twelve-tone technique and for organizing the millions of possibilities into 44 "tropes" (types) of tone rows in four groups based on symmetries among the unordered hexachords (with the prefixes Poly-, Mono-, Endo-, and Exo-).
After the first generation of "classic" serialists, we start to see a wider range of serial practices emerge, including a move toward "integral" or "total" serialism, which applies serial technique to parameters other than pitch, particularly rhythm, dynamics, and articulation. I say "after," but Ruth Crawford Seeger was already writing what later came to be known as integral or total serialism as early as c. 1930.
The most frequently cited examples came later, in a burst around 1950:
- Milton Babbitt: Three Compositions for Piano (1947)
- Olivier Messiaen: Mode de valeurs et dʼintensités for piano (1949–50)
- Karlheinz Stockhausen: Kreuzspiel for oboe, bass clarinet, piano, and two percussion (1951)
- Pierre Boulez: Structures 1 for two pianos (1952)
There were also signs of this mentality already in those "classic" early works. For instance, in the first movement of Webern’s Symphonie Op.21 (discussed further in this chapter), the exposition sees pitch classes fixed in specific registers, and his Op. 27 Variations for Piano has pitches, durations, and dynamics all aligned (for instance, B and G♯ are always eight notes, legato, and forte).
.front-matter h6 {
font-size: 1.25em;
}
.textbox--sidebar {
float: right;
margin: 1em 0 1em 1em;
max-width: 45%;
}
.textbox.textbox--key-takeaways .textbox__header p {
font: sans-serif !important;
font-weight: bold;
text-transform: uppercase;
font-style: normal;
font-size: larger;
}
a:link {
text-decoration: none;
}
button .a:link {
text-decoration: none;
color: white;
}
A term that summarizes the quality of the third, fifth, and seventh (if applicable) above the root of the chord. Common chord qualities are major, minor, diminished, half-diminished, dominant, and augmented.
Ordering the notes of a chord so that it is entirely stacked in thirds. The root of the chord is on the bottom.
Duplicating some notes of a chord in multiple parts.
Chromatic Modulation
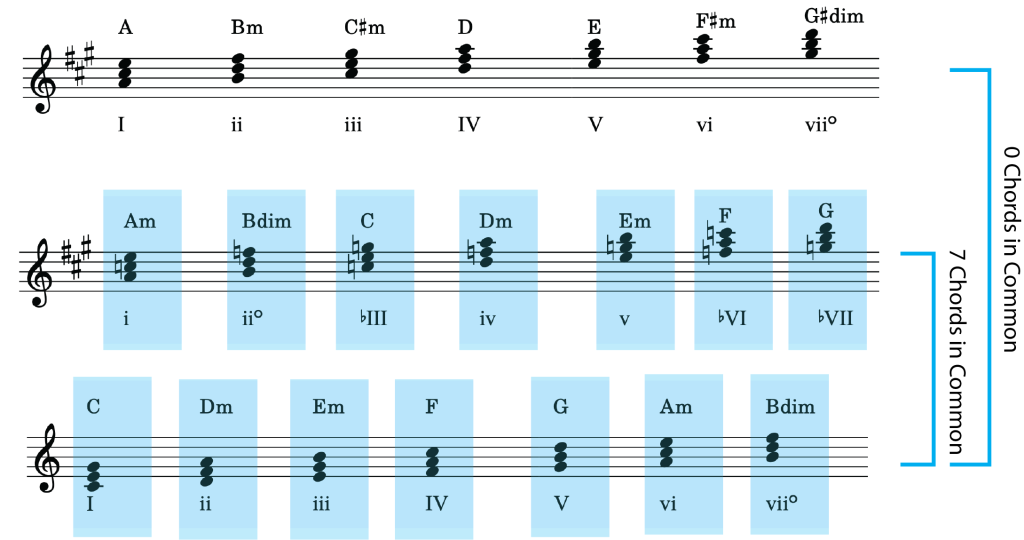
Modulation to closely-related keys is a relatively easy task; we can find a pivot chord by looking at the group of chords shared between two keys that have nearly-identical key signatures. There are plenty of them. For example:
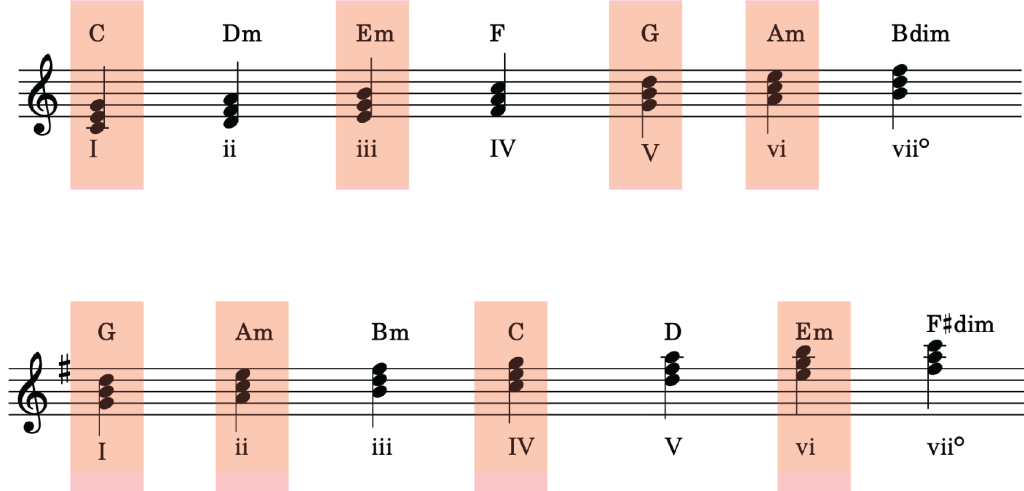
When two keys are more than one accidental apart on the circle of fifths, however, it becomes more difficult it is to find a pivot chord that will enable a smooth modulation between the two keys.
To modulate to a distantly-related key, that is, a key that is more than one accidental away on the circle of fifths, requires us to use our knowledge of chromatic chords, such as those found through mode mixture. Mode mixture enables us to expand the number of possible pivot chords for modulation. For example, in the key of C major, the chords made possible through mode mixture (i.e. those chords found in C minor, its parallel key), we can now modulate easily to E-flat major (7 shared chords), A-flat major (4 shared chords), B-flat major (3 shared chords), and their relative minor keys, F minor and G minor. Example 2 shows the common chords shared between C major and E-flat major, made possible by using mixture chords in C major.
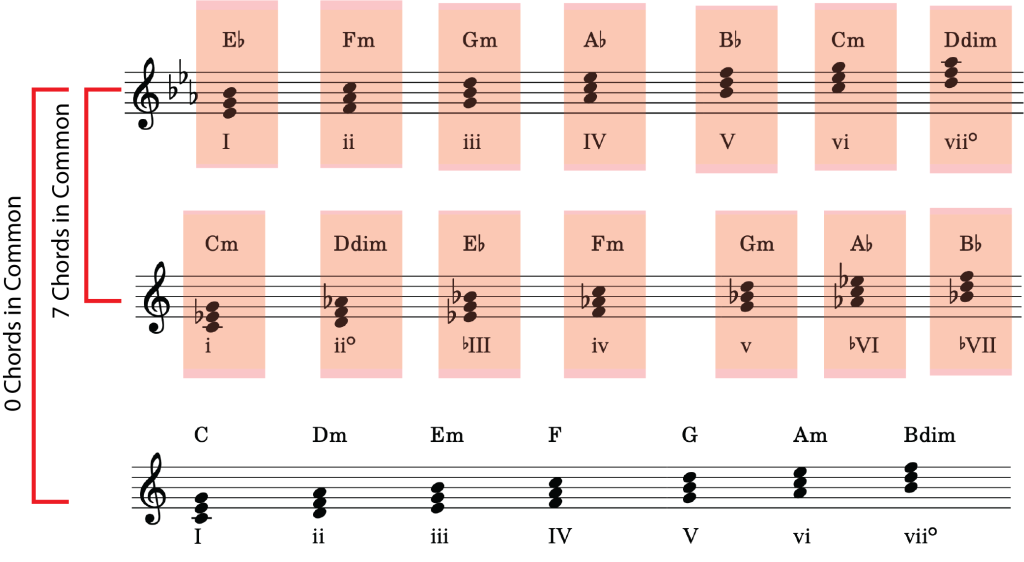Example 2. Shared chords between C major and E-flat major, made possible through mode mixture.
Example 3 shows a modulation from the key of A major to F major, using iv from A major as a pivot chord. Example 4 shows this technique being used by Verdi in his opera Rigoletto.
Example 3. Modulation from A major to F major using a mixture chord in A major (iv) as a pivot chord.
Example 4. Modulation from D-flat major to F-flat major using a mixture chord in Db major (bVI6) as a pivot chord.
Conversely, we can use diatonic chords in the old key as mixture chords in the new key to modulate to distant keys in the "sharpwise" direction on the circle of fifth. Example 5 shows the potential pivot chords when modulating from C major to A major by way of the diatonic chords in C major as mixture chords in the new key of A major.
Example 5. Potential pivot chords when modulating from C major to A major.
A modulation using this technique in a chorale setting is shown in Example 6.
Example 6. Modulation from A-flat major to C major using a diatonic chord in A-flat major (vi) as a pivot chord that is interpreted as a mixture chord (iv) in C major.
Example 7 shows an interesting chromatic modulation from Brahms's Waltz, op. 39, no. 14. Here, Brahms uses a diatonic viio6 chord in the local key of G major to pivot to E major, reinterpreting the chord as iio6, a mixture chord in the new key of E major.
Example 7. Modulation from G major to E major using a diatonic chord in G major (viio6) as a pivot chord that is interpreted as a mixture chord (iio6) in E major.
Common-Tone Modulation
Sometimes we can use a common-tone, rather than a pivot chord, to modulate to distantly related keys. In particular, the key areas that are a third away from the home key are easily modulated to using this technique.These keys, chromatically altered tonics that are a third away from the home key, are called “chromatic third” or “chromatic mediant” relations. For example:C and Ab major (share the common tone C), C and Eb major (share the common tone G), C and A major (share the common tone E), C and E major (share the common tone E).
Example 8. Common tones shared between chromatic mediants.
We can modulate to distant keys in several ways. Chromatic modulation refers to a modulation to a distant key by way of a chromatic chord. Enharmonic reinterpretation involves respelling and resolving a chromatic chord (usually a German augmented sixth or diminished seventh chord).
The German augmented-sixth chord may be respelled to resemble a dominant seventh chord. If you use the German augmented-sixth from the home key, the resulting modulation will be up a half step. Likewise, you can re- spell a dominant seventh chord to resemble a German augmented-sixth chord. If you use the dominant seventh chord in the home key, the resulting modulation will be down a half step. You can, of course, use this trick with any dominant-seventh chord (say, a secondary dominant), opening up numerous possibilities for modulation.
- Coming soon!
