6 Selected entries from Rhymes of Mathematical Times: 101 Mathematical Limericks
By Michael Matthews, Parker Lingelbach, and Craig Finlay
Sophie Germain
They said girls can’t do math at all
She wrote for the grand prize, not small –
as Monsieur LeBlanc,
so they wouldn’t honk,
while she walked away with the haul.

Sophie Germain (born April 1, 1776—died June 27, 1831) was a pioneering French mathematician known for her significant work in acoustics, elasticity, and the theory of primes. At the age of 13, she became fascinated with mathematics, despite this topic being considered inappropriate for women at the time. At 18 when the École Polytechnique opened, she obtained lecture notes, being unable to officially attend because of her gender. Being ostracized from the mathematical society for being a woman, she adopted the pseudonym of Monsieur LeBlanc when communicating with other mathematicians. There were two mathematicians she eventually confided in by revealing her identity: Lagrange and Gauss. Both mathematicians would give her guidance and praise, and Lagrange became her mentor.
In 1809, Germain started conducting experiments on vibrating metal plates for a competition organized by the Paris Academy of Sciences. In 1811, she submitted a paper but did not win, although Lagrange used Germain’s work to obtain an equation in his future work. Her second submission in 1813, received only an honorable mention as it was littered with mathematical errors. In 1816, she was awarded a prize by the Paris Academy of Sciences, becoming the first woman to receive this honor after submitting the paper under her own name. The prize consisted of a medal made of one kilogram of gold (about $100,000 in 2025 prices).
Germain’s most notable work is considered in number theory. Specifically, she proved the first case of the theorem for all odd primes p < 100. Additionally, she demonstrated a partial case for primes of the form 4n + 3 and established results that were later expanded upon, either decades or even centuries later.
Apollonius of Perga
Made cool shapes from slicing a cone –
parabolas, ellipses now known.
But what if instead –
he’d sliced some French bread,
Invented, alas, the first scone?

Apollonius of Perga (circa 262 BC—circa 190 BC) was a Greek mathematician often referred to as “The Great Geometer.” There are many works of Apollonius that have not survived time and are referred to by ancient writers. Some of the topics covered are limits for the value of 𝜋, irrationals, and polyhedrons. The surviving work that he is most known for is Conics, which is considered one of the most significant scientific contributions of the Hellenistic period. Conics was written in eight books, some surviving in Greek and others in Arabic. These books introduced the terms parabola, ellipse and hyperbola. His first four books contained results known to Euclid, Aristaeus, and others. However, Apollonius treatment of the fundamental properties of conics was much richer.” The last three books examine maximum and minimum lines, congruence and similarity, and diameters and their conjugates.
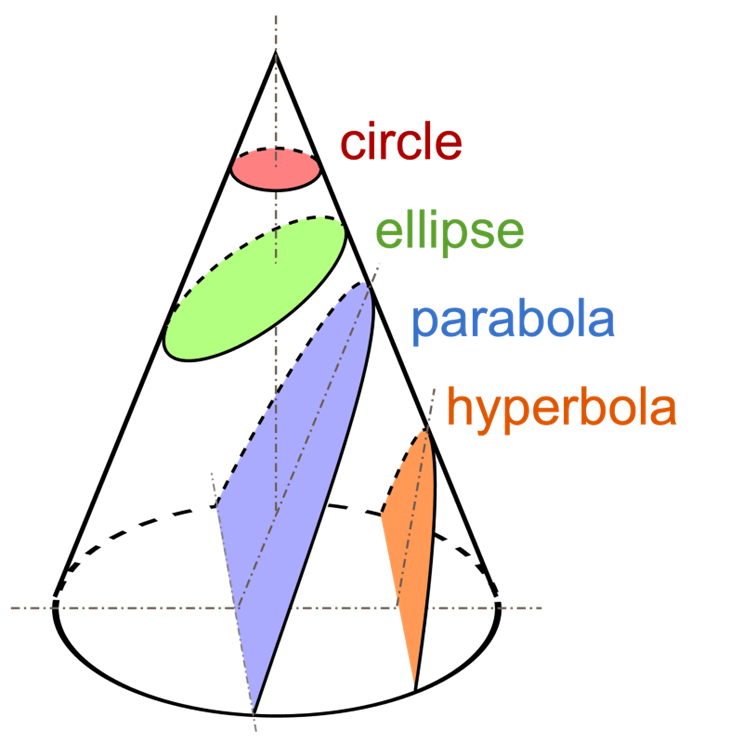
Morever, Apollonius gave us the term “conic sections”, which he defined as the curves formed when a plane (a flat, two-dimensional surface) intersects, or slices, the surface of a cone; see figure. Apollonius’ approach was different as he considered double oblique cones that extended indefinitely, while predecessors used finite circular right cones.
A scone is of a delicious baked good that is made into wedged (triangular) shapes by rolling dough into disks, then intersect the disks with a plane (aka a knife) to create the wedges.
Benjamin Banneker
His father a slave, but now free!
The son, a surveyor you see.
Math puzzles he made,
his neighbors then paid
for math jobs to solve over tea.

Benjamin Banneker (born November 9, 1731—died October 9, 1806) was a free African American naturalist, astronomer, surveyor, farmer, and mathematician. He was the son of a free black woman and a father who was a slave but was later freed. Despite limited formal education, he developed a strong interest in mathematics, astronomy, and mechanical engineering, which he pursued through self-study, and roughly three years at a Quaker school. As a young man, Banneker began to show his abilities when he created a clock from wood that gave precise time. It continued working for the rest of his life.
Banneker is best known for his work as a surveyor. In 1791, he was appointed to help survey the boundaries of the new federal capital, Washington D.C., which heavily relied on his knowledge of geometry and trigonometry. He was also known for his astronomical work, particularly his accurate prediction of a solar eclipse in 1789. His almanac, published in 1792, included astronomical calculations and was widely respected for its accuracy, especially for a black man during that era. The almanac included planetary placements, as well as the sun and the moon, and even a method for determining high tides in locations near Virginia and Maryland.
Being a well-respected figure in his community, Banneker would often entertain his neighbors with math problems, solving mathematical puzzles and offering his expertise in exchange for payment. He gained a reputation for exceptional mathematical abilities by frequently solving these problems or puzzles during social gatherings. Tragically, when the funeral for Banneker was held, his old farmhouse burnt to the ground. In the fire, only one of his manuscripts remained, containing the mathematical puzzles he created, with their solutions.
Bhaskara II
He surely did not have a peer,
with new math he did solve the year.
mere three minutes off,
you better not scoff
I doubt you could get it so near.

Bhaskara II or Bhaskaracharya (born 1114—died 1185) was an Indian polymath, mathematician and astronomer who was the first to create a work that systematically utilized the decimal system. To distinguish him from the 7th century astronomer Bhaskara I, the II is attached to his name, while the name Bhaskaracharya means “Bhaskara the Teacher”. He has six true works:
- Lilavati (The Beautiful)
- Bijaganita (Seed Counting or Root Extraction)
- Siddhanta Siromani (Crown of Treatises)
- Vasanabhasya of Mitaksara
- Karanakutuhala (Calculation of Astronomical Wonders)
- Vivarana
The preceding works of Bhaskara cover the topics of mathematics, algebra, mathematical astronomy and the sphere.
Most of Bhaskara’s works followed or filled gaps in Brahmagupta’s work. For example, using Brahmagupta’s astronomical model Bhaskara was able to accurately define many astronomical quantities including an approximation of the year’s length as 365.2588 days. The modern accepted measurement is 365.25636 days, which makes Bhaskara’s approximation off by about 3.5 minutes.
Often regarded as representing the pinnacle of mathematical knowledge in the 12th century, Bhaskara also wrote on calculus, trigonometry, and arithmetic. You can find his arithmetic work in the Lilavati which he dedicated to his daughter named Lilivati. When his dejected daughter discovered that she would never get married, the loving father Bhaskara decided to write her a mathematical manual so she would be remembered.
Lewis Carroll
He wrote of a grinning mad cat,
whose logic reversed in its chat.
Which way should I go?
Does it matter, though?
Each road will just end where it’s at.

Lewis Carroll is a pseudonym used by Charles Lutwidge Dodgson (born January 27, 1832—died January 14, 1898). He is best known as the author of Alice’s Adventures in Wonderland (1865) and Through the Looking Glass (1872). In his early life he had many struggles including an illness that left him deaf in one ear and years of suffering from bullies during his years at Rugby School (1846-50). In 1851, Caroll attended Christ Church, Oxford as an undergraduate where he studied and excelled in mathematics. Being at the head of his class in his mathematical finals, he obtained a Bachelor of Arts degree in 1854 and began teaching as a mathematics lecturer the following year.
As a mathematicians Carroll published his works under his true name, written as C L Dodgson. He authored many mathematics books covering topics such as plane algebraic geometry, plane trigonometry, determinants, arithmetic, parallels and books of Euclid. Of interest, Carroll wrote Euclid and his Modern Rivals (1879) in the style of a play. In it, Euclid appears as a ghost to defend his work against modern geometers.
Carroll’s work on logic included the development of a mechanical test of validity logic terms. He also employed truth tables to solve specific logic problems as early as 1894, even though truth tables and matrices became widely used only in 1920. Lastly, he developed the tree method for determining some validity by creating branching diagrams, which resemble the trees employed by his logician peers.
The grinning mad cat comes from Carroll’s Alice’s Adventures in Wonderland where you can find the Cheshire Cat engaging Alice in both amusing and perplexing conversation.
Hypatia of Alexandria
This pagan, she needs now to die.
She taught us to all wonder, “Why?”
Yet kill her you might,
because of your fright
Yet these truths they live still, they defy

Hypatia of Alexandria (born circa 370—died March 415) was an astronomer, mathematician, Neoplatonist philosopher, and the first female mathematician to have her life reasonably recorded. She was remembered on as a teacher and a wise counselor. There were serious religious conflicts in Alexandria during her life. Because of her Neoplatonist beliefs as well as her attachment to learning and science, some extreme Christians identified her as a pagan, although many others supported her. Though there are different accounts on Hypatia’s death, it is irrefutable that she was murdered by Christians who found her beliefs and knowledge threatening.
The daughter of the mathematician Theon of Alexandria, Hypatia collaborated with her father on Ptolemy’s Almagest and a revised version of Euclid’s Elements. Despite only assisting her father, some historians believe that she excelled Theon in mathematics and was a talented astronomer like him. Hypatia provided insights into Apollonius’s Conics, Diohpantus’s Arithmetica, and Ptolemy’s astronomical works, although some historians are skeptical about her commentaries on Ptolemy. When editing the work in Apollonius’s On the Conics of Apollonius, she made the concepts vastly easier to understand, helping the work survive through generations. It is said that none of Hypatia’s works have survived and all that is left are titles and references, but this claim is challenged by modern scholars that have identified several of her works.
There is no evidence of her own original mathematical works, and similarly there is no evidence that Hypatia has original works on philosophy. Instead of publishing original work, her and fellow scholars would comment on mathematical and philosophical works to develop their arguments.
John von Neumann
Please build us a big bomb, they asked.
Calculations, mistakes, all aghast.
A computer he made,
that helper and aid,
could do the mistakes really fast
John Von Neumann (born December 28, 1903—died February 8, 1957) was a Hungarian-born American mathematician, physicist, and pioneer of computer science. At a young age his brilliance was shown by entertaining guests through memorization games and his ability to exchange jokes in classical Greek. In 1922, he published his first mathematical paper with Michael Fekete after finishing his studies at the Lutheran Gymnasium in 1921. Von Neumann’s education continued at the University of Berlin until he moved to Zürich in 1923. He studied chemistry, and got a diploma in chemical engineering, but remained heavily interested in mathematics.
In the same year he received a diploma in chemical engineering, he obtained a doctorate in mathematics from the University of Budapest. He later became a mathematics professor with the likes of Einstein, J W Alexander, and H Weyl at the Institute for Advanced Study (IAS) in Princeton.
In the late 1930s von Neumann contributed to the Manhattan Project, and the creation of the atomic bomb. His work included calculations showing implosion would work, and despite his peer’s disbelief he continued its development. In 1945, with the help of George Kistiakowsky, the construction of the Trinity bomb was finished after many failed attempts.
During his work on the Manhattan project, John von Neumann played a pivotal role in the development of the computer. He helped conceptualize the creation of a computer that could store both its data and its program in the same address space. Based on the von Neumann architecture of the IAS, the MANIAC I was an early computer that was the first to defeat a human being in a chess-like game.
Johann Heinrich Lambert
A man of great sway, multinational.
He first showed us pi was irrational.
Not twenty-two sevenths,
nor any elevenths,
because we know pi’s not that fractional.

Johann Heinrich Lambert (born August 26, 1728—died September 25, 1777) was a physicist, astronomer, philosopher and mathematician who is perhaps best known for being the first to provide a rigorous proof that 𝜋 is irrational. Lambert was familiar with much of Europe. Born in France he spent time in Switzerland, Germany, Netherlands and Italy before dying in Prussia. He was largely self-educated, finding himself working to earn money for his family while he would purchase books to study in his own time. This studying eventually led him to become a tutor in Chur and elected to a Literary Society and to a Swiss Scientific Society.
Lambert’s first book was published in 1758, on the passage of light through various media. In 1760-1766, he published Photometria, Cosmologishe Briefe, Neues Organon, and Theorie der Parallellinien. The topics covered were the measurement of light, the universe, philosophy, and the parallel postulate. It was in 1768, when he presented to the Berlin Academy that 𝜋 is an irrational number. His proof claimed that if x is a nonzero rational number, then neither ex nor tan(x) can be rational. Since tan ![]() it follows that
it follows that ![]() must be irrational. Lambert also conjectured that 𝜋 is transcendental, but this was not proved until 1882 by Ferdinand von Lindemann.
must be irrational. Lambert also conjectured that 𝜋 is transcendental, but this was not proved until 1882 by Ferdinand von Lindemann.
This proof by Lambert was important because the mathematician Archimedes’ work led to widespread popular belief that 𝜋 is approximately ![]() and Lambert’s work refuted that. In 1898, Pringsheim noted that Lamberts proof was exceptional for its time as it also proved the tangent function to be a convergent continued fraction.
and Lambert’s work refuted that. In 1898, Pringsheim noted that Lamberts proof was exceptional for its time as it also proved the tangent function to be a convergent continued fraction.
Liu Hui
Taught math to sell millet and rice.
He wanted things fair, a good price.
We all pay some tax,
on our extra flax,
As long as I don’t pay it twice.
Liu Hui (born circa 220—died circa 280) was a Chinese mathematician best known for his commentary on the Jiuzhang suanshu (Nine Chapters on the Mathematical Art). No details about his personal life remain, but the book is of great historical interest. The exact authors and date of the original text remain unknown, but according to most historians it was written around 200 BC. This possible rewriting occurred after the ruler Qin Chih Huang tried to reform education by burning all books from prior learning. This text provided methods to solve everyday problems such as taxation, surveying, engineering, and trade.
The first chapter covers land surveying and gives 38 problems looking at area and fraction rules such as addition, subtraction, multiplication and division. Chapter two, named Millet and Rice, presents 46 problems related to the exchange rates of various grains, beans, and seeds. It introduces concepts of proportion and percentages, along with the rule of three for solving proportion-related problems. The next two chapters, four and five, contain 24 problems on short width, which asks what the length of a field is if the area is kept constant, but the width is increased, and 28 problems on civil engineering. Fair Distribution of Goods is the title of chapter six, where there are 28 problems involving ratio and proportions concerning travel, taxation, sharing, and more. The last three chapter titles are Excess and Deficit, Calculation by Square Tables and Right-angled triangles. Respectively, the chapters include 20, 18 and 24 problems.
The book Nine Chapters on the Mathematical Art in total includes 246 problems that played a fundamental role in the mathematical development of China, playing a similar role in the East as did Euclid’s Elements in the West.
Tartaglia and Cardano
He said that old Cardon did lie,
and published his work on the sly.
But here is the deal,
for some, roots aren’t real.
And they could not see i to i.

Niccolò Fontanta Tartaglia (born 1499—died December 13, 1557) was an Italian mathematician perhaps most famous for his work on ballistics and for discovering how to cubic equations without brute force efforts. This breakthrough took place in 1535, stemming from a challenge with the mathematician Fior. Each man was to send their counterpart 30 questions requiring cubic equations to be solved. The one-sided contest was over quickly due to Tartaglia’s discovery.
Girolamo Cardano (born September 24, 1501—died September 21, 1576) was an Italian mathematicians famed for his treatise Ars Magna. Upon hearing of Tartaglia and Fior’s contest, Cardano began seeking Tartaglia’s method of solving cubic equations. Cardano failed to ferret out the method so in 1539, through an intermediary, he asked Tartaglia if he could include his method in his next publication. Tartaglia first declined, wishing to publish it later, but with more offers from Cardano, he learned that this could be of great benefit for him considering Cardano’s powerful patrons.
In secrecy, Tartaglia divulged his formula, expressing that Cardano is to never reveal it. With the formula in hand, Cardano and his assistant began to make progress towards proofs for cubic and even quartic equations. Then, after learning that Tartaglia was not the first to discover how to solve the cubic equations, Cardano published it believing it would be of no harm to Tartaglia. Upon discovering the broken oath, Tartaglia presumed a never-ending hatred towards Cardano.
With the Cardano—Tartaglia formula, mathematicians can now solve cubic equations with complex numbers, denoted as ‘i’, and called the imaginary unit.
Full credit for photo of John von Neumann:
Unless otherwise indicated, this information has been authored by an employee or employees of the Los Alamos National Security, LLC (LANS), operator of the Los Alamos National Laboratory under Contract No. DE-AC52-06NA25396 with the U.S. Department of Energy. The U.S. Government has rights to use, reproduce, and distribute this information. The public may copy and use this information without charge, provided that this Notice and any statement of authorship are reproduced on all copies. Neither the Government nor LANS makes any warranty, express or implied, or assumes any liability or responsibility for the use of this information.
