7 Biostatistics for Parasitologists

Introduction

Students of veterinary or human epidemiology, evolutionary biologists, and ecologists alike, are often asked how heavily a particular host species (or population, or herd, etc.) is infected by parasites. Further questions arise in comparisons regarding which one is more infected, or which one is more subjected to more pathogenic pressure than the others. After carefully reading this chapter, you won’t be able to answer such questions–simply because such questions make no sense.

The occurrence of parasites within the host population, just like the harm exerted by them, is a complex pattern that cannot be described by a single statistical measure. Different indices capture different aspects of infection. Statistical indices have to be chosen that have clear (easy to understand) and distinct (non-overlapping) biological interpretations, and appropriate statistical tests must be chosen that are not based on assumptions that are not fulfilled in host-parasite systems. Unfortunately, some of the most widespread indices have vague if any biological interpretation, or they merely statistically predict each other, causing a redundancy of information.

Further, when applying appropriate indices to describe infection, it is a common situation that one index is higher in the host population A, the other index of infection is higher in population B, and so on. Even if all indices appear to be higher in one population than the other, we can never exclude the possibility that further meaningful indices can be proposed. A definite answer like “sample A is more infected than B” arises only in some rare and self-evident–and frankly not really interesting scientifically—cases when parasites are totally absent from the latter.

The aim of the present chapter is to advise readers how to choose appropriate statistical indices, and then, to choose the appropriate statistical tests to handle them. Finally, we offer a free statistical toolset to carry out the recommended statistical procedures in a relatively painless manner. The text below is based closely on a review paper by the authors of this chapter (Reiczigel et al., 2019a).

Taking Samples

Constrained by time, and financial and ethical limitations, investigators usually cannot collect and analyze every individual of a host-parasite system. Rather they take a random sample from the whole, with the hope that the sample will represent the unknown totality with reasonable accuracy. Of course, the larger the sample, the better accuracy we get. When taking a sample of a host-parasite system, typically, host individuals serve as ordinary units of sampling. First, a sample of host individuals is collected to represent the host population and, second, their bodies are searched for parasites. It is usually presumed that all parasites harbored by a particular host individual are found and identified, which may not be true.

Thus, we collect groups of parasite individuals inhabiting the same host individual, so-called parasite infrapopulations (Bush et al., 1997). Statistically speaking, random sampling of hosts implies cluster sampling of parasites. The size of these infrapopulations is most often expressed as the number of parasite individuals, thus we limit the discussion here to this particular situation.

Frequency Distribution of Host Individuals across Infection Classes

For sake of simplicity, first we focus our interest on the occurrence of a single species of parasite within a sample of hosts. After collecting a sample, all conspecific parasite individuals need to be identified and counted from each host. Then host individuals are characterized by the number of parasites they harbor, then they can be grouped into so-called infection classes, such as the group of non-infected hosts, the next group of hosts each harboring 1 parasite, the next group of those harboring 2 parasites, etc. Alternatively, wider categories are often applied, such as 0, 1–10, 11–20, etc. It is a common practice to replace the number of host individuals by the proportion (%) or probability (0–1 scale) that host individuals belong to a particular infection class. Such frequency distributions are visualized as histograms, and often used to characterize host-parasite systems.

Host-parasite frequency distributions do not approximate a normal distribution (a symmetric bell curve) nor a uniform distribution. Rather the distribution of parasites always exhibits an aggregated (also known as right-skewed, or positively-skewed) distribution: The majority of hosts harbor 0, or just a very few, parasites, a few hosts harbor more, and only a very few hosts harbor many more of them (see Figure 1; Crofton, 1971). The experienced frequency distributions, as visualized by histograms, can be approximated by mathematical models. In the case of natural infections by macroparasites, the so-called negative binomial distribution model often provides a good approximation.

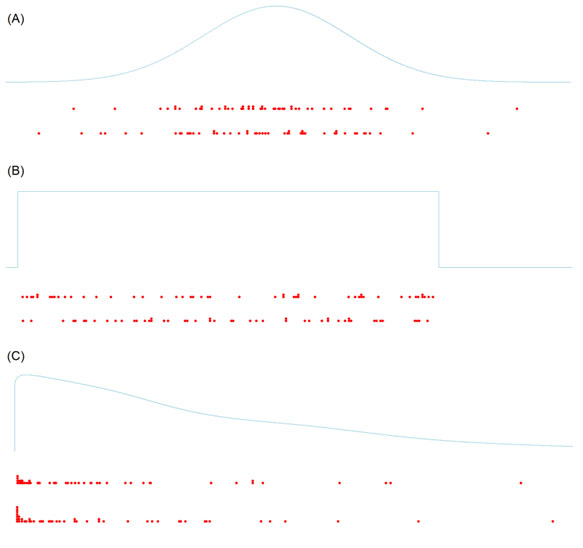
Figure 1. Density function (light blue) and dot plots of samples (n = 50) taken from different distributions. A) Normal distribution, where the mean is the most frequent value and the exceedingly smaller or greater values are exceedingly rare. B) Uniform distribution, where all values in a certain interval are equally likely. C) Aggregated (or right-skewed) distribution, where low values are frequent but high values are rare. Hosts grouped into parasite infection classes typically exhibit this type of distribution.
(Source: J. Reiczigel, M. Marozzi, F. Ibolya, and L. Rózsa. License: CC BY-NC-SA 4.0.)

Sample Size

Providing information on sample size is essential partly because it affects the accuracy of the sample estimates, and partly because low sample sizes tend to bias some of the estimated indices of infestation/infection (Reiczigel and Rózsa, 2017). Since hosts usually act as natural sampling units, authors typically express sample size as the number of host individuals. However, in certain cases (see below), the number of parasites collected/examined may remain totally unknown–a shortcoming that should be carefully avoided.

Prevalence

Prevalence (also called extensity in the early literature) is the proportion of infected individuals, traditionally expressed as a percentage (0–100% range) or as a probability (the probability that a randomly chosen individual is infected, 0–1 range). Sample prevalence is an estimate of the unknown true population prevalence and, thus, its 95% confidence interval (CI) must be calculated to express its precision or uncertainty: The wider the CI, the lower the precision of the estimate (or the higher the uncertainty).

There are several methods that can be used to calculate a CI for a proportion. It is traditional to apply the Clopper and Pearson’s (1934) method. Alternatively, Sterne’s (1954) method and Blaker’s (2000) method provide narrower, and thus more informative, interval estimates (see Reiczigel, 2003 for a comparison of their efficacy).

In epidemiology, the proportion of host individuals developing new infections within a specified period is called incidence or cumulative incidence. If calculated for a year (or month, week, etc.) it is called incidence rate or incidence density. The incidence expresses the risk of developing new infection in a certain time period. From a statistical point of view, incidence is handled similarly to prevalence, often modeled by the Poisson distribution.

Naturally, studies based on methods that can only differentiate the infected versus uninfected status of examined hosts (like serological methods) will report only sample size and prevalence (sample prevalence and its CI) to quantify results.

Mean Intensity

Intensity is the number of parasites found in an infected host. Sample mean intensity is the mean number of these values calculated for a sample, with all the 0 values of uninfected hosts excluded. Given the typical aggregated nature of parasite distributions, this value does not characterize a typical (say, characteristic, or usual) level of infection, rather it is highly dependent on the presence or absence of 1 or a very few highly infected host individuals. However, provided that sample size and prevalence are already known, mean intensity exactly defines the total number of parasites found in the sample. It is advisable to provide its 95% CI enabling readers to extrapolate it as an estimation of true population mean intensity. This CI is calculated by means of the bias-corrected and accelerated (BCa) bootstrap method of Efron and Tibshirani (1993).

Do not apply the scheme ‘mean ± SD,’ because it is meaningful only for symmetrical distributions, but not for the aggregated ones so characteristic to parasites. Thus, nonsense expressions like ‘mean intensity = 10 ± 20’ (erroneously suggesting that mean intensity can have negative values) are also avoided.

Before the era of computer-intensive methods, investigators often log-transformed raw values in order to normalize the data set. Then they calculated the mean of these transformed data, and statistically compared these means by parametric tests (like Student’s t test or ANOVA) applied on the log-scale, and finally back-transformed the mean and obtained the ‘geometric mean.’ However, log-transformed parasite distributions very poorly approximate the normal distribution model, and the resulting index, the ‘geometric mean’ of intensity is hard to interpret biologically. Given that computer-intensive methods like bootstrap have opened new avenues of statistical analyses, using geometric means should now be abandoned.

Median Intensity

Median intensity, unlike mean intensity, is not strongly affected by the values of the very few highly infected host individuals, thus it is more suitable to provide information about a typical (characteristic, usual) level of infection. Thus, while mean intensity (combining host sample size and prevalence) defines the number of parasites collected, median intensity informs about a characteristic state of infected hosts (of course, with the uninfected hosts excluded).

A 95% CI of median intensity is useful to express the accuracy of estimating population median intensity. For this purpose, the method introduced by Arnold et al. (2008) is followed. Due to the discreteness of data, it is often impossible to construct exact 95% confidence limits, thus, the shortest interval that reaches at least the desired confidence level is reported instead.

The most common method for the comparison of 2 medians is the non-parametric Wilcoxon-Mann-Whitney U-test (WMW). However, it should be noted that, without imposing some rather restrictive assumptions on the population distributions, WMW does not compare medians (there are examples where the sample medians are exactly equal and WMW detects a significant difference between the samples). One such assumption is that the frequency distributions to be compared have the same shape, the only difference between them is a shift along the horizontal axis (see Figure 2). There are other assumptions, but all of them are similarly restrictive, and most parasite distributions do not seem to fulfill them. If none of these assumptions hold, the result of the WMW test can be misleading (Divine et al., 2018). If the test detects a significant difference, the most one can say is that the distributions (rather than the means or medians) differ. Therefore, if differences between medians are of interest, the best choice is Mood’s Median Test (Sen, 1998).

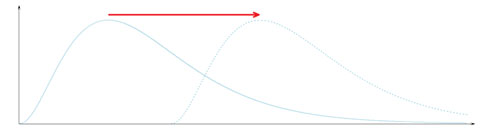
Figure 2. The classical assumption of the Wilcoxon-Mann-Whitney U-test is that the distributions to be compared have same shapes (and therefore same variances) but may be shifted along the horizontal axis (above). Unfortunately, real host-parasite systems do not fulfill this assumption, thus results of the WMW test are difficult to interpret.
(Source: J. Reiczigel, M. Marozzi, F. Ibolya, and L. Rózsa. License: CC BY-NC-SA 4.0.)

Stochastic Equality of Intensities or Abundances

The bootstrap test for stochastic equality of distributions (Reiczigel et al., 2005a) is a variant of the WMW test. It compares pairs of values taken from the 2 samples and tests whether the probability of getting higher values from one sample than from the other is same (50%–50%) or different. If using this method, the question regards only how often a value taken from one sample is higher than that from the other sample, but not how much higher. Therefore, if this test shows that infections in one sample tend to exceed those in the other, it does not necessarily mean that the latter sample hosts fewer parasites.

Abundance

Abundance is defined and treated similarly to intensity, but the 0 values of non-infected host individuals are not excluded. Due to the inclusion of the infection class 0 (noninfected hosts), the frequency distribution of abundance classes is more aggregated and, thus, their analysis is less accurate than that of the intensity classes, resulting in wider CIs and weaker statistical tests (greater p-values). Therefore, it is preferable to calculate intensity rather than abundance, and to avoid confusion, it is best to not provide both indices.

Presuming that sample size (N hosts) and prevalence are provided, readers already have all the information about the noninfected hosts, thus, the further inclusion of these calculations in quantitative descriptions is redundant. The relationship between mean abundance, mean intensity, and prevalence can be described by a simple formula, enabling calculation of any 1 of them when knowing the other 2 of them:

mean abundance = prevalence * mean intensity

Median abundance is a less informative measure, in particular, because, by definition, it equals 0 whenever prevalence is less than 50%, irrespective of the actual prevalence and the intensity values of infected hosts.
Overall, abundance measures (mean and median, their CIs) combine information on prevalence and intensity. Apply them only if such a combined index is definitely needed.

Crowding

Crowding is the size of the infrapopulation to which an individual parasite belongs (Reiczigel et al., 2005b). Although this equals intensity, intensity is defined as a host character, while crowding is a character of the parasite individual. Therefore, mean intensity refers to the intensity values averaged over host individuals, but mean crowding is obtained by averaging the crowding (= intensity) values over the parasite individuals. Say, mean intensity for 3 individuals infected by 1, 2, and 6 parasites is (1 + 2 + 6) / 3 = 3, while mean crowding for the parasites in the same sample is (1 + 2 + 2 + 6 + 6 + 6 + 6 + 6 + 6) / 9 = 4.56. Note that, due to the aggregated shape of distributions, an ‘average’ individual lives in a host that is more ‘crowded’ by conspecific parasites than the mean number of parasites per hosts (here: 4.56 > 3). Mean crowding is a rarely used index; however, it is a potentially meaningful measure of infection when speaking about density-dependent parasite characters (such as body size, fecundity, or sex ratio) in relation to the putative social environment of parasites.

Due to the usual sampling, that is, sampling the hosts, there are dependencies between the crowding values of parasite individuals: All of the conspecific parasites infecting the same host have identical values and, therefore, all of these values change simultaneously whenever a parasite is added or removed. This makes crowding values notoriously hard to handle statistically. As random sampling from the parasite population is practically infeasible, statistical methods assuming independence of the sample values—practically all classical methods, that is—cannot be validly used for the analysis of crowding.

A CI (confidence interval) for mean crowding can be created by the BCa bootstrap method as demonstrated by Efron and Tibshirani (1993). A 95% CI is useful to characterize the accuracy of sample mean crowding as an estimate of the true population value. Statistical comparisons of mean crowding across 2 (or more) different samples are also based on CIs. First, 97.5% CIs are generated for both samples. If these intervals overlap, the difference between the 2 samples is non-significant at the prescribed level of 0.05, that is, p > 0.05 (Reiczigel et al., 2005b). Unfortunately, the power of this testing method is rather low. Therefore, Neuhäuser and colleagues (2010) proposed applying Lepage’s (1971) location-scale test as a more suitable alternative.

From a purely mathematical point of view, diversity and crowding are closely related notions; one can be transformed into the other (Lang et al., 2017).

Levels of Aggregation

While all natural, and most experimental parasite infections exhibit an aggregated frequency distribution across host individuals, the level of aggregation may differ considerably from sample to sample. The most frequent indices to quantify these levels are, 1) The variance-to-mean ratio of abundance, 2) the exponent k of the negative binomial model fitted to the data (presuming acceptable fit of the model), and 3) Poulin’s (1993) ‘index of discrepancy,’ which includes a modified version of the so-called Gini-coefficient (a well known index in the literature of economics).
Although these indices aim to quantify the same feature (level of aggregation) of frequency distributions, unfortunately, their values do not exactly predict each other, thus, they cannot be transformed into each other and the are not interchangeable.

Just like in the case of mean crowding, these indices can be compared across samples by testing the potential overlap between their 97.5% CIs.

Parasite Sex Ratio

Samples of dioecious parasites can be characterized by their sex ratios. Note that the term sex ratio is quite misleading. Mathematically speaking, a ‘ratio’ should be expressed as the frequency of 1 sex divided by the frequency of the other sex. However, the index males/females would be unfavorable to apply; for example, it cannot be calculated for samples without females (since one cannot divide a number by 0). Instead, it is traditional to apply the proportion of males among adult dioecious parasites as a measure of sex ratio. Thus, the index called sex ratio actually means male-proportion. As it is a proportion, the recommended statistical tests are identical to those of prevalence.

Parasite Species Richness

Species richness is a simple and frequently used index to quantify diversity. Unfortunately, small samples tend to underestimate the true parasite species richness in populations of animals. General advice about the required sample size cannot be given because it depends on many other factors such as the levels of aggregation, interactions between parasite species, etc. There are several methods that have been designed to extrapolate sample values to the true parasite species richness harbored by the whole host population, so as to correct for this sample size bias. Walther and Morand (1998) compared the reliability of several methods using real parasitological datasets and found that the first-order jackknife (Heltshe and Forrester, 1983) and the Chao2 estimators performed best (Chao, 1987; Chao and Chiu, 2016). This latter method estimates the number of unobserved parasite species from the number of rare species (those occurring only in 1 or 2 hosts in the sample). Thus, the estimation fails in the absence of rare species in the sample, but it performs well if the number of rare species is < 50% of all parasite species in the dataset. It is also advised that a large sample of hosts is needed to obtain a reliable estimate, a sample size of at least a few hundred host individuals is recommended, but of course this depends on the estimated size of the population under study.

Interactions Between Parasite Species

Two parasite species coexisting in the same host population may exhibit a positive or negative interaction, making their co-occurrence in a particular host individual more or less likely than expected by chance. The simplest method to analyze such interactions is to summarize the presence or absence of the 2 species on each host in a 2 × 2 contingency table and apply Fisher’s Exact Test to analyze it. The sensitivity of this method, unfortunately, may be rather poor because the difference between hosting 0 or 1 parasite individuals is often negligible. Therefore, computing the Spearman Rank Correlation coefficient to explore potential interactions between abundance values of the 2 parasite species is recommended as it provides a more robust or sensitive estimate.

Quantitative Parasitology on the Web (QPweb)

Misuse of biostatistics and misinterpretation of statistical results are very common in the parasitological literature. Therefore, we have published a brief overview of the suitable biostatistical tools together with some new methods proposed by us (Rózsa et al., 2000) to address these important issues. The Rózsa et al. (2000) paper was accompanied by freely distributed software called Quantitative Parasitology (QP) to make the recommended statistical procedures easily accessible. Subsequent software versions QP1.0, QP2.0, and QP3.0 followed with increasing numbers of new functions. These were made available as downloadable software that ran on Windows PCs. Each was capable of handling only 1 type of parasite per host sample, thus, multispecies infections or sex ratios could not be analyzed. Finally, we introduced Quantitative Parasitology on the Web (QPweb) in 2013, which is an R-based interactive web service capable of communicating with computers via an internet browser, independently of the operating system used. Contrary to former versions, this one is already capable of representing different types of parasites (different species, different sexes, and so on) co-occurring in the same host sample, opening new possibilities for analyzing parasite communities.

Parallel to the introduction of subsequent software versions, we also published new biostatistical procedures potentially useful in characterizing the infection level of a sample or comparing infection indices across samples of hosts (Reiczigel, 2003; Reiczigel et al., 2005a; 2005b; 2008). All these new procedures were incorporated into the newer software versions. The latest version of QPweb (v1.0.15, as of 2020, and still in 2024) is freely available on the web (Reiczigel et al., 2019b; available at https://www2.univet.hu/qpweb/qp10/index.php) to carry out most of the procedures mentioned above, including a simple users’ guide to help work through potential technical difficulties (Figure 3).

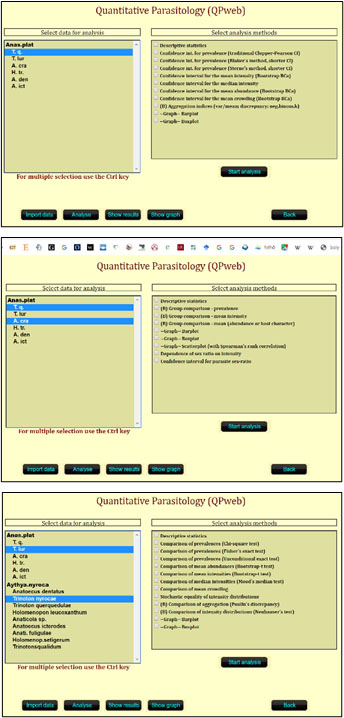
Figure 3. Analysis tools offered by QPweb when choosing different combinations of samples. Top: One species of parasite in 1 sample of host. Middle: Two species of parasites in 1 sample of host. Bottom: Two species of parasites in 2 samples of hosts.
(Source: J. Reiczigel, M. Marozzi, F. Ibolya, and L. Rózsa. License: CC BY-NC-SA 4.0.)

Literature Cited

Arnold, B. C., N. Balakrishnan, and H. N. Nagaraja. 2008. A First Course Order in Statistics. Society for Industrial and Applied Mathematics, Philadelphia, Pennsylvania, United States, 279 p.

Blaker, H. 2000. Confidence curves and improved exact confidence intervals for discrete distributions. Canadian Journal of Statistics 28: 783–798. doi: 10.2307/3315916

Bush, A. O., K. D. Lafferty, J. M. Lotz, and A. W. Shostak. 1997. Parasitology meets ecology on its own terms: Margolis et al. revisited. Journal of Parasitology 83: 575–583. doi: 10.2307/3284227

Chao, A. 1987. Estimating the population size for capture data with unequal catchability. Biometrics 43: 783–791. doi: 10.2307/2531532

Chao, A., and C. H. Chiu. 2016. Bridging the variance and diversity decomposition approaches to beta diversity via similarity and differentiation measures. Methods in Ecology and Evolution 7: 919–928. doi: 10.1111/2041-210X.12551

Clopper, C. J., and E. S. Pearson. 1934. The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 26: 404–413. doi: 10.1093/biomet/26.4.404

Crofton, H. D. 1971. Quantitative approach to parasitism. Parasitology 62: 179–193. doi: 10.1017/S0031182000071420

Divine, G. W., H. J. Norton, A. E. Barón, and E. Juarez-Colunga. 2018. The Wilcoxon-Mann-Whitney procedure fails as a test of medians. American Statistician 72: 278–286. doi: 10.1080/00031305.2017.1305291

Efron, B., and R. Tibshirani. 1993. An Introduction to the Bootstrap. Chapman and Hall, New York, New York, United States, 456 p.

Heltshe, J. F., and N. E. Forrester. 1983. Estimating species richness using the jackknife procedure. Biometrics 39: 1–11. doi: 10.2307/2530802

Lang, Z., L. Rózsa, and J. Reiczigel. 2017. Comparison of measures of crowding, group size and diversity. Ecosphere 8: e01897. doi: 10.1002/ecs2.1897

Lepage, Y. 1971. A combination of Wilcoxon’s and Ansari-Bradley’s statistics. Biometrika 58: 213–217. doi: 10.2307/2334333

Neuhäuser, M., J. Kotzmann, M. Walier, and R. Poulin. 2010. The comparison of mean crowding between two groups. Journal of Parasitology 96: 477–481. doi: 10.1645/GE-2177.1

Poulin, R. 1993. The disparity between observed and uniform distributions: A new look at parasite aggregation. International Journal for Parasitology 23: 937–944. doi: 10.1016/0020-7519(93)90060-C

Reiczigel, J. 2003. Confidence intervals for the binomial parameter: Some new considerations. Statistics in Medicine 22: 611–621. doi: 10.1002/sim.1320

Reiczigel, J., and L. Rózsa. 2017. Do small samples underestimate mean abundance? It depends on what type of bias we consider. Folia Parasitologica 64: 025. doi: 10.14411/fp.2017.025

Reiczigel, J., Z. Abonyi, and J. Singer. 2008. An exact confidence set for two binomial proportions and exact unconditional confidence intervals for the difference and ratio of proportions. Computational Statistics and Data Analysis 52: 5,046–5,053. doi: 10.1016/j.csda.2008.04.032

Reiczigel, J., Z. Lang, L. Rózsa, and B. Tóthmérész. 2005a. Properties of crowding indices and statistical tools to analyze crowding data. Journal if Parasitology 91: 245–252. doi: 10.1645/GE-281R1

Reiczigel, J., M. Marozzi, I. Fábián, and L. Rózsa. 2019a. Biostatistics for parasitologists: A primer to Quantitative Parasitology. Trends in Parasitology 35: 277–281. doi: 10.1016/j.pt.2019.01.003

Reiczigel, J., L. Rózsa, J. Reiczigel, and F. Ibolya. 2019b. Quantitative Parasitology (QPweb), version 1.0.15. https://www2.univet.hu/qpweb/qp10/index.php

Reiczigel, J., I. Zakariás, and L. Rózsa. 2005b. A bootstrap test of stochastic equality of two populations. American Statistician 59: 156–161. doi: 10.1198/000313005X23526

Rózsa, L., J. Reiczigel, and G. Majoros. 2000. Quantifying parasites in samples of hosts. Journal of Parasitology 86: 228–232. doi: 10.1645/0022-3395(2000)086[0228:QPISOH]2.0.CO;2

Sen, P. K. 1998. Multivariate median and rank sum tests. In P. Armitage and T. Colton, eds. Encyclopedia of Biostatistics, Volume IV. Wiley, Chichester, United Kingdom, p. 2,887–2,900. doi: 10.1002/0470011815.b2a13052

Sterne, T. E. 1954. Some remarks on confidence or fiducial limits. Biometrika 41: 275–278. doi: 10.2307/2333026

Walther, B. A., and S. Morand. 1998. Comparative performance of species richness estimation methods. Parasitology 116: 395–405. doi: 10.1017/S0031182097002230