IV. Diatonic Harmony, Tonicization, and Modulation
57
John Peterson and Megan Lavengood
Key Takeaways
- Tonicization is the process of making a non-tonic chord sound like a temporary tonic. This is done with chromatic chords called applied chords, or secondary dominant chords (V(7)) and secondary leading-tone chords (viio(7)) borrowed from the temporary key.
- Applied chords are notated with a slash. The chord before the slash is the identity of the applied chord within the secondary key, and the chord after the slash is the chord being tonicized. It’s read aloud from left to right with the word “of” replacing the slash: V/ii becomes “five of two.”
- Applied chords nearly always involve accidentals, and especially accidentals that raise the pitch.
- Another way of thinking about applied chords is to imagine them as altered versions of the diatonic chord with which it shares a root (for example, ii becomes II♯, which is V/V).
Tonicization is the process of making a non-tonic chord temporarily sound like tonic. It’s accomplished using secondary dominant or secondary leading-tone chords (sometimes called applied dominant and applied leading-tone chords). First, we’ll learn how to tonicize the dominant, and then we’ll see tonicizations of non-dominant chords.
Tonicizing V
Analyzing tonicization
Secondary dominant chords (V(7)/V)
Example 1 analyzes a passage that temporarily makes V sound like the tonic chord. Example 2 extracts the two chords from Example 1 that participate in the tonicization. We have a C7 chord moving to an F chord, so if we were to analyze these chords without considering the key signature or the context that Example 1 provides, we’d say the two chords represent the progression [latex]\mathrm{V^6_5-I}[/latex] in F major (Example 2a).
https://musescore.com/user/32728834/scores/6268930/embed
Example 1. Tonicization in Joseph Bologne, Six Concertante Quartets, no. 1, II, mm. 1–8.
https://musescore.com/user/32728834/scores/6268934/embed
Example 2. Reduction of the tonicization in Joseph Bologne, Six Concertante Quartets, no. 1, II, mm. 3–4.
If we now reconsider the context that Example 1 provides, we can see that the F major chord functions as V in the excerpt’s home key of B♭ major (Example 2b). Indeed, it’s the chord that creates the half cadence that ends the first phrase. We know that we haven’t changed keys here because, in addition to the half cadence being in B♭ major, the second phrase also begins in B♭ major (it repeats the beginning of the first phrase). The C7 chord, however, clearly doesn’t belong to B♭ major—that’s what the E♮ accidental in the bass tells us. As we determined in Example 2, the C7 chord is [latex]\mathrm{V^6_5}[/latex] of the F major chord. To represent that in the context of Example 1, we say that the C7 chord is “[latex]\mathrm{V^6_5}[/latex] of V,” and we write “[latex]\mathrm{V^6_5/V}[/latex].” In other words, the F major chord is V, and the C7 chord is the [latex]\mathrm{V^6_5}[/latex] of that V chord. We’ve just labeled our first secondary dominant chord!
Secondary leading-tone chords (viio(7)/V)
Tonicization can also be accomplished using secondary leading-tone chords, as in Example 3.
https://musescore.com/user/32728834/scores/6268967/embed
Example 3. Tonicization in Josephine Lang, “Du gleichst dem klaren blanen See,” mm. 21–24.
https://musescore.com/user/32728834/scores/6268972/embed
Example 4. Reduction of the tonicization in Josephine Lang.
Example 4 walks through how to understand the relationship between the two highlighted chords in Example 3.
- If we were in G major, we would analyze these chords as viio7–I. Recall that when we learned about the leading-tone seventh chord, we discovered that it’s common to lower the chordal seventh in major to create a fully diminished seventh chord. That’s still true here (notice the E♭!).
- The passage in Example 3 is in C major, so we would analyze the G major chord as V, rather than I. That means the F♯o7 chord is viio7 of the V chord. We write “viio7/V” and say “seven diminished seven of five.”
- The passage in Example 3 adds a [latex]\mathrm{cad.^6_4}[/latex] to embellish the dominant. That’s why the viio7/V doesn’t resolve directly to V.
- The [latex]\mathrm{cad.^6_4}[/latex] resolves to V7 rather than the V triad. Now we’ve arrived at the passage in Example 3.
Summary: Steps for analyzing tonicization
Chromaticism is an indication that tonicization may be present. Since only V(7) and viio7 (or, rarely, vii∅7—see note in sidebar) can create tonicization, one of the most helpful things for determining the label is to ask “what is the quality of the chromatic chord?” The quality determines the label: if the chord is a major triad or dominant seventh chord, it gets the label V(7). If the chord is a diminished triad or diminished seventh chord, it gets the label viio(7).
When you come across a chromatic note, stop and ask the following questions:
- Is the chromatic note part of the chord, or is it an embellishing tone?
- Part of the chord: move on to question 2
- Embellishing tone: label appropriately
- What’s the quality of the chord?
- Major triad or dominant seventh chord: secondary V chord; label is V(7)/x
- Diminished triad or diminished seventh: secondary viio chord; label is viio7/x
- To determine x above, ask: In what key is the chromatic chord V or viio? Then, determine what Roman numeral the tonic triad of that key would get in the home key of your passage. That Roman numeral is x.
Writing applied chords
Spelling
The video in Example 5 walks through the steps for spelling V7/V, viio7/V, and vii∅7/V in major and minor keys. We recommend you grab a piece of staff paper so you can follow along by pausing the video and trying the exercises yourself. The steps are summarized below:
- Determine the root of the chord being tonicized
- Pretend this root is the tonic of a temporary key
- Spell the top Roman numeral in that key (either V7 or viio7)
Example 5. Steps for spelling applied chords.
Resolving
The leading tone of the applied chord is referred to as the secondary leading tone; the chordal seventh is referred to as the secondary seventh. These dissonances resolve just as they normally would in their own key.
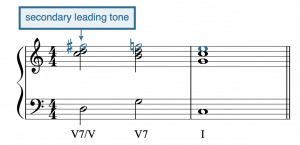
One exception is that when the tonicized chord is itself a seventh chord (as in the progression D7–G7–C), the secondary leading tone may resolve down by semitone into the seventh of the following chord. In the example progression, this would create a nice chromatic line: F♯–F♮–E (Example 6).
The video in Example 7 walks through the steps for spelling V7/V, viio7/V, and vii∅7/V in major and minor keys. Like with the previous video, we recommend pausing to try each exercise on staff paper. The steps are summarized below:
- Spell the secondary chord
- Follow the typical writing procedure to part-write, but think in the temporary new key to determine how tendency tones resolve
- Check accidentals (especially if in minor)
Example 7. Steps for resolving applied chords.
Tonicizing chords other than V
Overview
Any major or minor triad can be tonicized, not just V. Diminished and augmented triads can’t be tonicized, since there are no diminished or augmented keys. This means that every Roman numeral can be tonicized except viio and iio.
Analyzing various tonicizations
When chords other than V are tonicized, we follow the same steps for analysis that we learned earlier; the only difference is that there are now more possibilities for which chords can be tonicized. Be on the lookout for chromatic notes: these are signals that tonicization may be present!
As you might imagine, the frequency with which a given chord is tonicized is related to the frequency with which that chord generally appears. For instance, the dominant and strong predominant chords are quite common, so we also see those chords tonicized with some frequency. The vi chord, while less common than ii, IV, and V, also frequently gets tonicized. The iii and VII (minor only) chords are uncommon harmonies, and we tend not to see them tonicized frequently.
Tonicizing strong predominants
Tonicizing strong pre-dominants usually involves chromatic inflection of members of the tonic triad. For example, a tonic triad can easily be turned into a V7/IV chord by adding te [latex](\downarrow\hat7)[/latex] to the triad (Example 8). Similarly, a tonic triad can be turned into viio7/ii by raising do ([latex]\hat{1}[/latex]) and adding te [latex](\downarrow\hat7)[/latex] (Example 9).
https://musescore.com/user/32728834/scores/6270521/embed
Example 8. Tonicizing IV in Joseph Bologne, String Quartet no. 4, I, mm. 41–47 (1:18–1:30).
https://musescore.com/user/32728834/scores/6270540/embed
Example 9. Tonicizing ii in Maria Szymanowska, Minuet no. 4, mm. 57–64 (1:48–1:55).
Tonicized deceptive motion
One striking way to use tonicization is to highlight a deceptive motion (Example 10). Here, the dominant moves to viio7/vi before the vi chord arrives, which draws our attention even more to the absence of the expected tonic after the V chord.
https://musescore.com/user/32728834/scores/6270545/embed
Example 10. Tonicized deceptive motion in Josephine Lang, “Mag da draussen Sehnee,” mm. 1–5.
Adding tonicization to diatonic progressions
The steps for part-writing tonicization remain the same as for tonicizations of V. Now, however, we should expect to see tonicizations of non-dominant major and minor triads. Example 11 shows a diatonic progression (a) to which several tonicizations have been added (b).
https://musescore.com/user/32728834/scores/6270553/embed
Example 11. Adding tonicizations to a diatonic progression.
Secondary dominants as altered diatonic chords
Another way of thinking about secondary chords is to imagine them as altered versions of the diatonic chord with which it shares a root.
The most straightforward example is when a ii chord is chromatically altered by changing fa ([latex]\hat{4}[/latex]) to fi ([latex]\uparrow\hat{4}[/latex]) and then progresses, like usual, to the dominant chord. This alteration of fa to fi [latex](\hat4-\uparrow\hat4)[/latex] turns a regular subdominant chord into a chord that has a dominant function in the key of the dominant.
Take the chord progression Dmi7–G–C in C major, which we would label with Roman numerals as ii7–V–I. If we change fa to fi ([latex]\hat4[/latex] to [latex]\uparrow\hat4[/latex], F to F♯) in the first chord, we get D7–G–C. In the key of C, we might analyze this progression as II♯7–V–I(note the uppercase Roman numeral, indicating the change of quality; the sharp sign afterward further clarifies the raised third of the chord). However, we can also note that D major belongs to G major; it is a dominant-functioning chord (V) in the key of G—the key in which the following chord is tonic. In other words, we are borrowing the dominant chord from the key of G and applying it to the G-major triad. Thus, we can re-interpret the progression as V7/V–V–I.
Practice it!
Example 12 summarizes secondary chords as they relate to diatonic chords with the same root.
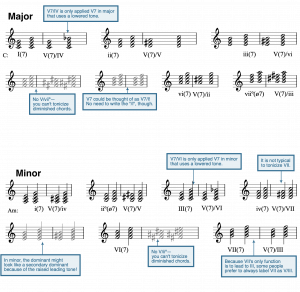
- Applied chords worksheet, available in three slightly different versions:
- Version A (.pdf, .mscx). Asks students to identify and write applied V, V7, viio, viio7, and vii∅7 chords with Roman numerals and figures.
- Version B—without ∅7s (.pdf, .mscz). Asks students to identify and write applied V, V7, viio, and viio7 chords with Roman numerals and figures.
- Version C—jazz/pop focus (.pdf, .mscz). No ∅7s or figured bass; all chords in root position. Students identify and write chord symbols in addition to notation.
- All applied chords (.pdf, .docx). Asks students to write from Roman numerals and figured bass, write from a longer figured bass, and analyze a complete piece with discussion questions.
A chord from another key inserted into a new key, in order to tonicize a diatonic chord other than I.
A chromatic chord that temporarily tonicizes another key besides the tonic key, by taking on a dominant function in that new key.
Key Takeaways
- A beat is a pulse in music that regularly recurs.
- Simple meters are meters in which the beat divides into two, and then further subdivides into four.
- Duple meters have groupings of two beats, triple meters have groupings of three beats, and quadruple meters have groupings of four beats.
- There are different conducting patterns for duple, triple, and quadruple meters.
- A measure is equivalent to one group of beats (duple, triple, or quadruple). Measures are separated by bar lines.
- Time signatures in simple meters express two things: how many beats are contained in each measure (the top number), and the beat unit (the bottom number), which refers to the note value that is the beat.
- A beam visually connects notes together, grouping them by beat. Beaming changes in different time signatures.
- Notes below the middle line on a staff are up-stemmed, while notes above the middle line on a staff are down-stemmed. Flag direction works similarly.
In Rhythmic and Rest Values, we discussed the different rhythmic values of notes and rests. Musicians organize rhythmic values into various meters, which are—broadly speaking—formed as the result of recurrent patterns of accents in musical performances.
Terminology
Listen to the following performance by the contemporary musical group Postmodern Jukebox ( Example 1). They are performing a cover of the song "Wannabe" by the Spice Girls (originally released in 1996). Beginning at 0:11, it is easy to tap or clap along to this recording. What you are tapping along to is called a beat—a pulse in music that regularly recurs.
Example 1. A cover of "Wannabe" performed by Postmodern Jukebox; listen starting at 0:11.
Example 1 is in a simple meter: a meter in which the beat divides into two, and then further subdivides into four. You can feel this yourself by tapping your beat twice as fast; you might also think of this as dividing your beat into two smaller beats.
Different numbers of beats group into different meters. Duple meters contain beats that are grouped into twos, while Triple meters contain beats that are grouped into threes, and Quadruple meters contain beats that are grouped into fours.
Listening to Simple Meters
Let's listen to examples of simple duple, simple triple, and simple quadruple meters. A simple duple meter contains two beats, each of which divides into two (and further subdivides into four). "The Stars and Stripes Forever" (1896), written by John Philip Sousa, is in a simple duple meter.
Listen to Example 2, and tap along, feeling how the beats group into sets of two:
Example 2. "The Stars and Stripes Forever" played by the Dallas Winds.
A simple triple meter contains three beats, each of which divides into two (and further subdivides into four). Wolfgang Amadeus Mozart's "Minuet in F major," K.2 (1774) is in a simple triple meter. Listen to Example 3, and tap along, feeling how the beats group into sets of three:
Example 3. Mozart's "Minuet in F major," played by Alan Huckleberry.
Finally, a simple quadruple meter contains four beats, each of which divides into two (and further subdivides into four). The song "Cake" (2017) by Flo Rida is in a simple quadruple meter. Listen to Example 4 starting at 0:45 and tap along, feeling how the beats group into sets of four:
Example 4. "Cake" by Flo Rida; listen starting at 0:45.
As you can hear and feel (by tapping along), musical compositions in a wide variety of styles are governed by meter. You might practice identifying the meters of some of your favorite songs or musical compositions as simple duple, simple triple, or simple quadruple; listening carefully and tapping along is the best way to do this. Note that simple quadruple meters feel similar to simple duple meters, since four beats can be divided into two groups of two beats. It may not always be immediately apparent if a work is in a simple duple or simple quadruple meter by listening alone.
Conducting Patterns
If you have ever sung in a choir or played an instrument in a band or orchestra, then you have likely had experience with a conductor. Conductors have many jobs. One of these jobs is to provide conducting patterns for the musicians in their choir, band, or orchestra. Conducting patterns serve two main purposes: first, they establish a tempo, and second, they establish a meter.
The three most common conducting patterns outline duple, triple, and quadruple meters. Duple meters are conducted with a downward/outward motion (step 1), followed by an upward motion (step 2), as seen in Example 5. Triple meters are conducted with a downward motion (step 1), an outward motion (step 2), and an upward motion (step 3), as seen in Example 6. Quadruple meters are conducted with a downward motion (step 1), an inward motion (step 2), an outward motion (step 3), and an upward motion (step 4), as seen in Example 7:
Beat 1 of each of these measures is considered a downbeat . A downbeat is conducted with a downward motion, and you may hear and feel that it has more "weight" or "heaviness" then the other beats. An upbeat is the last beat of any measure. Upbeats are conducted with an upward motion, and you may feel and hear that they are anticipatory in nature.
Example 8 shows a short video demonstrating these three conducting patterns:
Example 8. Dr. John Lopez (Texas A&M University, Kingsville) demonstrates duple, triple, and quadruple conducting patterns.
You can practice these conducting patterns while listening to Example 2 (duple), Example 3 (triple), and Example 4 (quadruple) above.
Time Signatures
In Western musical notation, beat groupings (duple, triple, quadruple, etc.) are shown using bar lines, which separate music into measures (also called bars), as shown in Example 9. Each measure is equivalent to one beat grouping.

In simple meters, time signatures (also called meter signatures) express two things: 1) how many beats are contained in each measure, and 2) the beat unit (which note value gets the beat). Time signatures are expressed by two numbers, one above the other, placed after the clef (Example 10).

A time signature is not a fraction, though it may look like one; note that there is no line between the two numbers. In simple meters, the top number of a time signature represents the number of beats in each measure, while the bottom number represents the beat unit.
In simple meters, the top number is always 2, 3, or 4, corresponding to duple, triple, or quadruple beat patterns. The bottom number is usually one of the following:
- 2, which means the half note gets the beat.
- 4, which means the quarter note gets the beat.
- 8, which means the eighth note gets the beat.
You may also see the bottom number 16 (the sixteenth note gets the beat) or 1 (the whole note gets the beat) in simple meter time signatures.
There are two additional simple meter time signatures, which are 𝄴 (common time) and 𝄵 (cut time). Common time is the equivalent of [latex]\mathbf{^4_4}[/latex] (simple quadruple—four beats per measure), while cut time is the equivalent of [latex]\mathbf{^2_2}[/latex] (simple duple—two beats per measure).
Counting in Simple Meter
Counting rhythms aloud is important for musical performance; as a singer or instrumentalist, you must be able to perform rhythms that are written in Western musical notation. Conducting while counting rhythms is highly recommended and will help you to keep a steady tempo. Please note that your instructor may employ a different counting system. Open Music Theory privileges American traditional counting, but this is not the only method.
Example 11 shows a rhythm in a [latex]\mathbf{^4_4}[/latex] time signature, which is a simple quadruple meter. This time signature means that there are four beats per measure (the top 4) and that the quarter note gets the beat (the bottom 4).
- In each measure, each quarter note gets a count, expressed with Arabic numerals—"1, 2, 3, 4."
- When notes last longer than one beat (such as a half or whole note in this example), the count is held over multiple beats. Beats that are not counted out loud are written in parentheses.
- When the beat in a simple meter is divided into two, the divisions are counted aloud with the syllable “and,” which is usually notated with the plus sign (+). So, if the quarter note gets the beat, the second eighth note in each beat would be counted as “and.”
- Further subdivisions at the sixteenth-note level are counted as “e” (pronounced as a long vowel, as in the word “see”) and “a” (pronounced “uh”). At the thirty-second-note level, further subdivisions add the syllable “ta” in between each of the previous syllables.
Example 11. Rhythm in 4/4 time.
Simple duple meters have only two beats and simple triple meters have only three, but the subdivisions are counted the same way (Example 12).
Example 12. Simple duple meters have two beats per measure; simple triple meters have three.
Like with notes that last for two or more beats, beats that are not articulated because of rests, ties, and dots are also not counted out loud. These beats are usually written in parentheses, as shown in Example 13:
Example 13. Beats that are not counted out loud are put in parentheses.

When an example begins with a pickup note (anacrusis), your count will not begin on "1," as shown in Example 14. An anacrusis is counted as the last note(s) of an imaginary measure. When a work begins with an anacrusis, the last measure is usually shortened by the length of the anacrusis. This is demonstrated in Example 14: the anacrusis is one quarter note in length, so the last measure is only three beats long (i.e., it is missing one quarter note).
Counting with Beat Units of 2, 8, and 16
In simple meters with other beat units (shown in the bottom number of the time signature), the same counting patterns are used for the beats and subdivisions, but they correspond to different note values. Example 15 shows a rhythm with a [latex]\mathbf{^4_4}[/latex] time signature, followed by the same rhythms with different beat units. Each of these rhythms sounds the same and is counted the same. They are also all considered simple quadruple meters. The difference in each example is the bottom number of the time signature—which note gets the beat unit (quarter, half, eighth, or sixteenth).
Example 15. The same counted rhythm, as written in a meter with (a) a quarter-note beat, (b) a half-note beat, (c) an eighth-note beat, and (d) a sixteenth-note beat.
Beaming, Stems, Flags, and Multi-Measure Rests
Beams connect notes together by beat. As Example 16 shows, this means that beaming changes depending on the time signature. In the first measure, sixteenth notes are grouped into sets of four, because four sixteenth notes in a [latex]\mathbf{^4_4}[/latex] time signature are equivalent to one beat. In the second measure, however, sixteenth notes are grouped into sets of two, because one beat in a [latex]\mathbf{^4_8}[/latex] time signature is only equivalent to two sixteenth notes.
Example 16. Beaming in two different meters.

Note that in vocal music, beaming is sometimes only used to connect notes sung on the same syllable. If you are accustomed to music without beaming, you may need to pay special attention to beaming conventions until you have mastered them. In the top staff of Example 17, the eighth notes are not grouped with beams, making it difficult to see where beats 2 and 3 in the triple meter begin. The bottom staff shows that if we re-notate the rhythm so that the notes that fall within the same beat are grouped together with a beam, it makes the music much easier to read. Note that these two rhythms sound the same, even though they are beamed differently. The ability to group events according to a hierarchy is an important part of human perception, which is why beaming helps us visually parse notated musical rhythms—the metrical structure provides a hierarchy that we show using notational tools like beaming.
Example 18 shows several different note values beamed together to show the beat unit. The first line does not require beams because quarter notes are never beamed, but all subsequent lines do need beams to clarify beats.
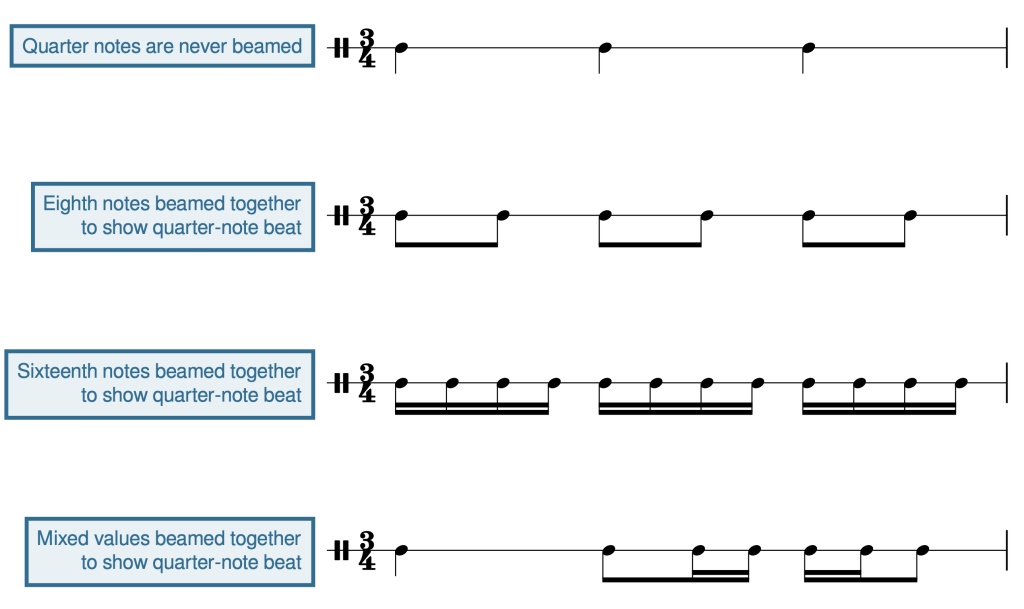

The second measure of Example 19 shows that when notes are grouped together with beams, the stem direction is determined by the note farthest from the middle line. On beat 1 of measure 2, this note is E5, which is above the middle line, so down-stems are used. Beat 2 uses up-stems because the note farthest from the middle line is the E4 below it.

Flagging is determined by stem direction (Example 20). Notes above the middle line receive a down-stem (on the left) and an inward-facing flag (facing right). Notes below the middle line receive an up-stem (on the right) and an outward-facing flag (facing left). Notes on the middle line can be flagged in either direction, usually depending on the contour of the musical line.
Partial beams can be used for mixed rhythmic groupings, as shown in Example 21. Sometimes these beaming conventions look strange to students who have had less experience with reading beamed music. If this is the case, you will want to pay special attention to how the notes in Example 21 are beamed.
Example 21. Partial beams are used for some mixed rhythmic groupings.
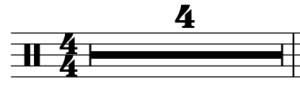
Rests that last for multiple full measures are sometimes notated as seen in Example 22. This example indicates that the musician is to rest for a duration of four full measures.
A Note on Ties
We have already encountered ties that can be used to extend a note over a measure line. But ties can also be used like beams to clarify the metrical structure within a measure. In the first measure of Example 23, beat 2 begins in the middle of the eighth note, making it difficult to see the metrical structure. Breaking the eighth note into two sixteenth notes connected by a tie, as shown in the second measure, clearly shows the beginning of beat 2.
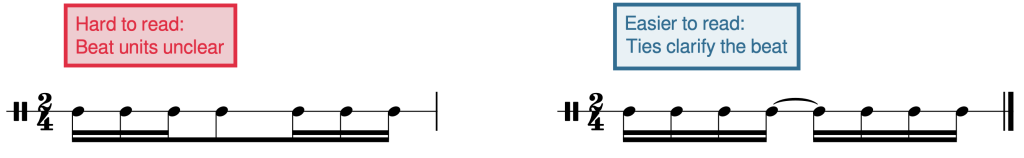
- Simple Meter Tutorial (musictheory.net)
- Video Tutorial on Simple Meter, Beats, and Beaming (YouTube)
- Conducting Patterns (YouTube)
- Simple Meter Time Signatures (liveabout.com)
- Video Tutorial on Counting Simple Meters (One Minute Music Lessons)
- Simple Meter Counting (YouTube)
- Beaming Rules (Music Notes Now)
- Beaming Examples (Dr. Sebastian Anthony Birch)
- Time Signatures and Rhythms (.pdf)
- Terminology, Bar Lines, Fill-in-rhythms, Re-beaming (.pdf)
- Meters, Time Signatures, Re-beaming (website)
- Bar Lines, Time Signatures, Counting (.pdf)
- Time Signatures, Re-beaming, p. 4 (.pdf)
- Fill-in-rhythms (.pdf)
- Time Signatures (.pdf, .pdf)
- Bar Lines (.pdf, .pdf, .pdf)
At the end of each chapter, you may find Assignments linked for that chapter. Those same assignments are also gathered here in a single table for convenient browsing.
Use arrows in the cells on the header row to sort the table alphabetically. Use the "Search" function to filter by the words in your search.
Last updated: [table “65” not found /]
[table “65” not found /]
| Book order | Part | Chapter | Assignments |
|---|---|---|---|
| 1 | I. Fundamentals | Introduction to Western Musical Notation |
|
| 2 | I. Fundamentals | Notation of Notes, Clefs, and Ledger Lines |
|
| 3 | I. Fundamentals | Reading Clefs |
|
| 4 | I. Fundamentals | The Keyboard and the Grand Staff |
|
| 5 | I. Fundamentals | Half Steps, Whole Steps, and Accidentals |
|
| 6 | I. Fundamentals | American Standard Pitch Notation (ASPN) |
|
| 7 | I. Fundamentals | Other Aspects of Notation |
|
| 8 | I. Fundamentals | Notating Rhythm |
|
| 9 | I. Fundamentals | Simple Meter and Time Signatures |
|
| 10 | I. Fundamentals | Compound Meter and Time Signatures |
|
| 11 | I. Fundamentals | Other Rhythmic Essentials |
|
| 12 | I. Fundamentals | Major Scales, Scale Degrees, and Key Signatures |
|
| 13 | I. Fundamentals | Minor Scales, Scale Degrees, and Key Signatures |
|
| 14 | I. Fundamentals | Introduction to Diatonic Modes and the Chromatic “Scale” |
|
| 15 | I. Fundamentals | Intervals |
|
| 16 | I. Fundamentals | Triads |
|
| 17 | I. Fundamentals | Seventh Chords |
|
| 18 | I. Fundamentals | Inversion and Figured Bass |
|
| 19 | I. Fundamentals | Roman Numerals and SATB Chord Construction | |
| 20 | I. Fundamentals | Texture |
|
| 21 | II. Counterpoint and Galant Schemas | Introduction to Species Counterpoint |
|
| 22 | II. Counterpoint and Galant Schemas | First-Species Counterpoint |
|
| 23 | II. Counterpoint and Galant Schemas | Second-Species Counterpoint |
|
| 24 | II. Counterpoint and Galant Schemas | Third-Species Counterpoint |
|
| 25 | II. Counterpoint and Galant Schemas | Fourth-Species Counterpoint |
|
| 26 | II. Counterpoint and Galant Schemas | Fifth-Species Counterpoint |
|
| 27 | II. Counterpoint and Galant Schemas | Gradus ad Parnassum Exercises | |
| 28 | II. Counterpoint and Galant Schemas | 16th-Century Contrapuntal Style |
|
| 29 | II. Counterpoint and Galant Schemas | High Baroque Fugal Exposition |
|
| 30 | II. Counterpoint and Galant Schemas | Ground Bass |
|
| 31 | II. Counterpoint and Galant Schemas | Galant Schemas – Summary | |
| 32 | II. Counterpoint and Galant Schemas | Galant schemas – The Rule of the Octave and Harmonizing the Scale with Sequences |
|
| 33 | II. Counterpoint and Galant Schemas | Galant Schemas |
|
| 34 | III. Form | Foundational Concepts for Phrase-Level Forms |
|
| 35 | III. Form | The Phrase, Archetypes, and Unique Forms |
|
| 36 | III. Form | Hybrid Phrase-Level Forms |
|
| 37 | III. Form | Expansion and Contraction at the Phrase Level |
|
| 38 | III. Form | Formal Sections in General | |
| 39 | III. Form | Binary Form |
|
| 40 | III. Form | Ternary Form |
|
| 41 | III. Form | Sonata Form |
|
| 42 | III. Form | Rondo |
|
| 43 | IV. Diatonic Harmony, Tonicization, and Modulation | Introduction to Harmony, Cadences, and Phrase Endings |
|
| 44 | IV. Diatonic Harmony, Tonicization, and Modulation | Strengthening Endings with V7 |
|
| 45 | IV. Diatonic Harmony, Tonicization, and Modulation | Strengthening Endings with Strong Predominants |
|
| 46 | IV. Diatonic Harmony, Tonicization, and Modulation | Embellishing Tones |
|
| 47 | IV. Diatonic Harmony, Tonicization, and Modulation | Strengthening Endings with Cadential 6/4 |
|
| 48 | IV. Diatonic Harmony, Tonicization, and Modulation | Prolonging Tonic at Phrase Beginnings with V6 and Inverted V7s | |
| 49 | IV. Diatonic Harmony, Tonicization, and Modulation | Performing Harmonic Analysis Using the Phrase Model |
|
| 50 | IV. Diatonic Harmony, Tonicization, and Modulation | Prolongation at Phrase Beginnings using the Leading-Tone Chord |
|
| 51 | IV. Diatonic Harmony, Tonicization, and Modulation | 6/4 Chords as Forms of Prolongation |
|
| 52 | IV. Diatonic Harmony, Tonicization, and Modulation | Plagal Motion as a Form of Prolongation |
|
| 53 | IV. Diatonic Harmony, Tonicization, and Modulation | La (Scale Degree 6) in the Bass at Beginnings, Middles, and Endings |
|
| 54 | IV. Diatonic Harmony, Tonicization, and Modulation | The Mediant Harmonizing Mi (Scale Degree 3) in the Bass |
|
| 55 | IV. Diatonic Harmony, Tonicization, and Modulation | Predominant Seventh Chords |
|
| 56 | IV. Diatonic Harmony, Tonicization, and Modulation | Tonicization |
|
| 57 | IV. Diatonic Harmony, Tonicization, and Modulation | Extended Tonicization and Modulation to Closely Related Keys |
|
| 58 | V. Chromaticism | Modal Mixture |
|
| 59 | V. Chromaticism | Neapolitan 6th (♭II6) |
|
| 60 | V. Chromaticism | Augmented Sixth Chords |
|
| 61 | V. Chromaticism | Common-Tone Chords (CTº7 & CT+6) |
|
| 62 | V. Chromaticism | Harmonic Elision |
|
| 63 | V. Chromaticism | Chromatic Modulation |
|
| 64 | V. Chromaticism | Reinterpreting Diminished Seventh Chords |
|
| 65 | V. Chromaticism | Augmented Options |
|
| 66 | V. Chromaticism | Equal Divisions of the Octave |
|
| 67 | V. Chromaticism | Chromatic Sequences |
|
| 68 | V. Chromaticism | Parallel Chromatic Sequences |
|
| 69 | V. Chromaticism | The Omnibus Progression |
|
| 70 | V. Chromaticism | Altered and Extended Dominant Chords |
|
| 71 | V. Chromaticism | Neo-Riemannian Triadic Progressions |
|
| 72 | V. Chromaticism | Mediants |
|
| 73 | VI. Jazz | Swing Rhythms |
|
| 74 | VI. Jazz | Chord Symbols |
|
| 75 | VI. Jazz | Jazz Voicings |
|
| 76 | VI. Jazz | ii–V–I | |
| 77 | VI. Jazz | Embellishing Chords |
|
| 78 | VI. Jazz | Substitutions |
|
| 79 | VI. Jazz | Chord-Scale Theory |
|
| 80 | VI. Jazz | Blues Harmony |
|
| 81 | VI. Jazz | Blues Melodies and the Blues Scale |
|
| 82 | VII. Popular Music | Rhythm and Meter in Pop Music |
|
| 83 | VII. Popular Music | Drumbeats |
|
| 84 | VII. Popular Music | Melody and Phrasing |
|
| 85 | VII. Popular Music | Introduction to Form in Popular Music | |
| 86 | VII. Popular Music | AABA Form and Strophic Form |
|
| 87 | VII. Popular Music | Verse-Chorus Form |
|
| 88 | VII. Popular Music | Introduction to Harmonic Schemas in Pop Music | |
| 89 | VII. Popular Music | Blues-Based Schemas |
|
| 90 | VII. Popular Music | Four-Chord Schemas |
|
| 91 | VII. Popular Music | Classical Schemas (in a Pop Context) |
|
| 92 | VII. Popular Music | Puff Schemas |
|
| 93 | VII. Popular Music | Modal Schemas |
|
| 94 | VII. Popular Music | Pentatonic Harmony |
|
| 95 | VII. Popular Music | Fragile, Absent, and Emergent Tonics |
|
| 96 | VIII. 20th- and 21st-Century Techniques | Twentieth-Century Rhythmic Techniques | |
| 97 | VIII. 20th- and 21st-Century Techniques | Pitch and Pitch Class |
|
| 98 | VIII. 20th- and 21st-Century Techniques | Intervals in Integer Notation |
|
| 99 | VIII. 20th- and 21st-Century Techniques | Pitch-Class Sets, Normal Order, and Transformations |
|
| 100 | VIII. 20th- and 21st-Century Techniques | Set Class and Prime Form |
|
| 101 | VIII. 20th- and 21st-Century Techniques | Interval-Class Vectors |
|
| 102 | VIII. 20th- and 21st-Century Techniques | Analyzing with Set Theory (or not!) |
|
| 103 | VIII. 20th- and 21st-Century Techniques | Diatonic Modes |
|
| 104 | VIII. 20th- and 21st-Century Techniques | Collections |
|
| 105 | VIII. 20th- and 21st-Century Techniques | Analyzing with Modes, Scales, and Collections |
|
| 106 | IX. Twelve-Tone Music | Basics of Twelve-Tone Theory |
|
| 107 | IX. Twelve-Tone Music | Naming Conventions for Rows |
|
| 108 | IX. Twelve-Tone Music | Row Properties |
|
| 109 | IX. Twelve-Tone Music | Analysis Examples – Webern Op. 21 and 24 | |
| 110 | IX. Twelve-Tone Music | Composing with Twelve Tones |
|
| 111 | IX. Twelve-Tone Music | History and Context of Serialism | |
| 112 | X. Orchestration | Core Principles of Orchestration |
|
| 113 | X. Orchestration | Subtle Color Changes |
|
| 114 | X. Orchestration | Transcription from Piano |
|
| 115 | XI. Rhythm and Meter | Notating Rhythm [crosslist] |
|
| 116 | XI. Rhythm and Meter | Simple Meter and Time Signatures [crosslist] |
|
| 117 | XI. Rhythm and Meter | Compound Meter and Time Signatures [crosslist] |
|
| 118 | XI. Rhythm and Meter | Other Rhythmic Essentials [crosslist] |
|
| 119 | XI. Rhythm and Meter | Hypermeter |
|
| 120 | XI. Rhythm and Meter | Metrical Dissonance |
|
| 121 | XI. Rhythm and Meter | Swing Rhythms [crosslist] |
|
| 122 | XI. Rhythm and Meter | Rhythm and Meter in Pop Music [crosslist] |
|
| 123 | XI. Rhythm and Meter | Drumbeats [crosslist] |
|
| 124 | XI. Rhythm and Meter | Twentieth-Century Rhythmic Techniques [crosslist] |
|
A symbol that alters a pitch, such as the sharp (♯), flat (♭), and natural (♮) symbols.
The process by which a non-tonic triad is made to sound like a temporary tonic. It involves the use of secondary dominant or leading-tone chords.
Relating in some sense to the chromatic scale. The term may be used to refer to notes that are outside the given key.
A 7̂ that is one half step below 1̂. The leading tone is diatonic in major keys, but requires an accidental in minor keys.
Altered dominant chords
Altered dominant chords feature either an augmented or diminished fifth. Augmented fifths are indicated in analysis by “+” beside the Roman numeral. Diminished fifths are indicated by a “o” beside the Roman numeral.
Dominant with an augmented fifth
If you raise the fifth of a dominant triad, it will become an augmented triad. Typically, raised fifths resolve upward by step to the third of its target chord. Note that the augmented triad is a symmetrical chord than can be interpreted in multiple ways, making it difficult to identify its root without proper surrounding context. Like the diminished-seventh chord, this means that the augmented triad can be a pathway to distant, chromatic modulations. See Example 1, which shows the three possible enharmonic interpretations and resolutions of the C augmented triad.
Importantly, these chords do not resolve easily to minor triads, since the augmented fifth would not be able to resolve upward by step.
Example 1: The three possible resolutions of the C augmented triad.
The Dominant with Diminished Fifth
When you add a 7th to a Vo chord, you get a chord that sounds precisely like a French augmented-sixth chord. This equivalence becomes even clearer when you use the Vo7 chord in second inversion, leaving the lowered fifth in the bass voice to resolve downward by step. As Example 2 shows, the chords Vo4/3/V and the French augmented-sixth chord are identical.
Example 2: The dominant chord with a diminished fifth, and its equivalence with the French augmented-sixth chord.
Extended dominant chords
Extensions can be added to dominant chords to create new and interesting sonorities. These chords are typically found only in root position.
When composing these chords in a four-voice texture, you need to decide which notes to leave out. These chords will always include the root and the chordal seventh.
The V9 chord replaces a doubled root with a ninth. The ninth should resolve down by step.
The V11 chord replaces the third with an eleventh. The eleventh “resolves” by common-tone. This chord typically includes both the ninth and the eleventh, and resembles a IV chord with scale-degree 5 in the bass.
The V13 chord replaces the fifth with a thirteenth. The thirteenth “resolves” by leaping down by third to scale-degree 1.
- Coming soon!
.front-matter h6 {
font-size: 1.25em;
}
.textbox--sidebar {
float: right;
margin: 1em 0 1em 1em;
max-width: 45%;
}
.textbox.textbox--key-takeaways .textbox__header p {
font: sans-serif !important;
font-weight: bold;
text-transform: uppercase;
font-style: normal;
font-size: larger;
}
.button {
background: gray;
}
A harmonic function that may either lead toward a dominant-function chord or back to a tonic-function chord. Subdominant function is most typically associated with the IV chord, otherwise known as the subdominant chord, and the II chord, otherwise known as the supertonic chord.

